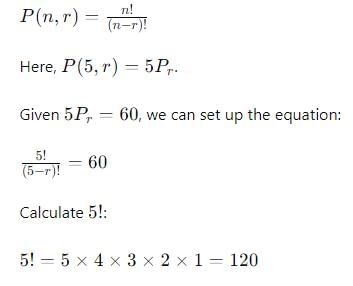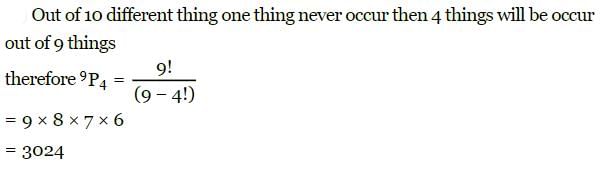Test: Permutations and Combinations- 1 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Permutations and Combinations- 1
Choose the most appropriate option (a) (b) (c) or (d)
4P3 is evaluated as
In nPr = n (n–1) (n–2) ………………(n–r–1), the number of factor is
If . nP3 : nP2 = 3 : 1, then n is equal to
The number of ways the letters of the word COMPUTER can be arranged is
The number of arrangements of the letters in the word FAILURE, so that vowels are always coming together is
10 examination papers are arranged in such a way that the best and worst papers never come together. The number of arrangements is
n articles are arranged in such a way that 2 particular articles never come together. The number of such arrangements is
If 12 school teams are participating in a quiz contest, then the number of ways the first, second and third positions may be won is
The sum of all 4 digit number containing the digits 2, 4, 6, 8, without repetitions is
The number of 4 digit numbers greater than 5000 can be formed out of the digits 3,4,5,6 and 7(no. digit is repeated). The number of such is
4 digit numbers to be formed out of the figures 0, 1, 2, 3, 4 (no digit is repeated) then number of such numbers is
The number of ways the letters of the word “Triangle” to be arranged so that the word ’angle’ will be always present is
If the letters word ‘Daughter ’ are to be arranged so that vowels occupy the odd places, then number of different words are
The number of ways in which 7 girls form a ring is
The number of ways in which 7 boys sit in a round table so that two particular boys may sit together is
In how many ways can 10 examination papers be arranged so that the best and the worst papers never come together?
3 ladies and 3 gents can be seated at a round table so that any two and only two of the ladies sit together. The number of ways is
The number of ways in which the letters of the word DOGMATIC can be arranged is
The number of arrangements of 10 different things taken 4 at a time in which one particular thing always occurs is
The number of permutations of 10 different things taken 4 at a time in which one particular thing never occurs is
|
101 videos|277 docs|89 tests
|



 is equal to
is equal to  is a symbol equal to
is a symbol equal to