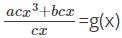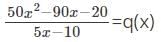Test: Polynomial Division - ACT MCQ
10 Questions MCQ Test - Test: Polynomial Division
If the polynomial f(x) = x2 + kx - 15, is exactly divisible by x - 5, then the value of k is _______
The real number that should be subtracted from the polynomial f(x) = 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 so that it is exactly divisible by 5x4 + 10x3 - 15x2 - 5x is ____________
The polynomial (x), if the divisor is 5x2, quotient is 2x + 3, and remainder is 10x + 20 is __________
What will be the value of a and b if the polynomial f(x) = 30x4 - 50x3 + 109x2 - 23x + 25, when divided by 3x2 - 5x + 10, gives 10x2 + 3 as quotient and ax + b as remainder?
If α is a zero of the polynomial f(x), then the divisor of f(x) will be _________
What real number that should be added to the polynomial f(x) = 81x2 - 31, so that it is exactly divisible by 9x + 1?
When a polynomial f(x) = acx3 + bcx + d, is divided by g(x), it leaves quotient as cx, and remainder as d. The value of g(x)will be _____
The quotient if the polynomial f(x) = 50x2 - 90x - 25 leaves a remainder of -5, when divided by 5x - 10, will be __________
If two of the zeros of the polynomial f(x) = x3 + (6 - √3)x2 + (-1 - √3)x + 30 - 6√3 are 3 and -2 then, the other zero will be ____________
If f(x) is divided by g(x), it gives quotient as q(x) and remainder as r(x). Then, f(x) = q(x) × g(x) + r(x) where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.