Test: Polynomials (Medium) - Class 10 MCQ
20 Questions MCQ Test - Test: Polynomials (Medium)
Find the zeros of a quadratic polynomial √3x2 - 8x + 4√3.
Find the smallest solution in positive integers of x2 - 14y2 = 1.
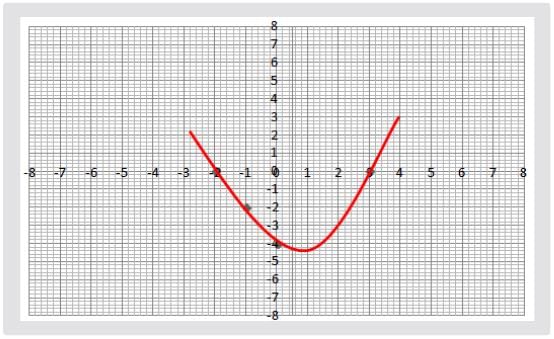
Find the zeroes of the quadratic polynomial from the graph.
If one zero of polynomial (k2 + 16) x2 + 16x + 8k is reciprocal of the other, them k is equal to
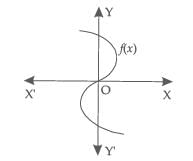
The graph of f(x) is shown below. The number of zeroes of f(x) are:
The graph of a quadratic polynomial p(x) = ax2 + bx + c is a parabola, opening downwards if
Sum of the zeroes of the polynomial p(x) = - 3x2 + a is
The sum and product of zeroes of a quadratic polynomial are - 1 and - 6 respectively. The quadratic polynomial is given by
Number of quadratic polynomials having - 2 and - 5 as their two zeroes is
Which of the following is not a graph of a quadratic polynomial?
If one zero of the quadratic polynomial 39 y2 - (2k + 1)y - 22 is negative of the other, then the value of k is
If α and β are zeros of a quadratic polynomial such that α + β = 12 and α - β = 6. Them, the family of quadratic polynomials having α, β as its zeroes is given by
If α, β, γ are the zeroes of the polynomial p(x) = x3 + 6x2 + cx + d, such that α + β = 2, then the value of γ is
If the zeroes of the quadratic polynomial x2 + (a +1) x + b are 2 and - 3, then
When x4 + x3 - 2x2 + x + 1 is divided by x - 1, them the remainder is
If α and β are the zeroes of the quadratic polynomial p(x) = x2 + 2x - k such that α2 + β2 = 34, then the value of k is
If the sum of products of zeroes taken, two at a time of polynomial p(x) = x3 - 5x2 + kx + 8 is 2, then the value of k is




















