Test: Probability (संभाव्यता) - 1 - UPSC MCQ
10 Questions MCQ Test CSAT Topic Wise Mock Tests (Hindi) 2025 - Test: Probability (संभाव्यता) - 1
एक बैग में 5 वर्गाकार बक्से और 7 बेलनाकार बक्से हैं । दो बक्से यादृच्छिक तरीके से निकाले गए हैं । इसकी क्या प्रायिकता है कि वे एक ही आकार के हों?
52 कार्डों के एक पैकेट पर विचार करें । एक कार्ड यादृच्छिक तरीके से निकाला गया है । कार्ड के पान या सात होने की प्रायिकता क्या है?
दो पासे एक साथ फेंक दिए जाते हैं | दो संख्याओं के प्राप्त करने की प्रायिकता क्या है, जिसका योग विषम हो?
मान लीजिए कि एक लड़की एक डाई (पासा) फेंकती है यदि 5 या 6 आता है, तो उसने तीन बार सिक्का टॉस किया और हेड की संख्या को लिखा । अगर उसे 1, 2, 3 या 4 मिलता है, तो उसने एक बार सिक्का टॉस किया और नोट किया कि हेड या टेल में से कौनसा प्राप्त हो रहा है । यदि वह निश्चित रूप से एक हेड प्राप्त कर लेती है, तो इसकी संभावना क्या है कि उसने पासा फेंकने पर 1, 2, 3 या 4 प्राप्त किया?
पासा को दो बार फेंकने से आये परिणाम के योग के 6 आने की संभावना क्या है?
दो पासे फेंके गये हैं | इसकी क्या संभावना है सभी अभाज्य संख्यायेँ नहीं है?
52 कार्ड के पैक से यादृच्छिक रूप से दो कार्ड निकाले गए हैं, इसकी क्या संभावना है कि दोनों लाल हो या दोनों जैक हैं?
एक कक्षा में, 30% छात्र अंग्रेजी में उत्तीर्ण हुए और 20% छात्र हिंदी में उत्तीर्ण हुए और 10% दोनों में उत्तीर्ण हुए । यदि किसी छात्र को यादृच्छिक रूप से चुना जाता है, तो उसके अंग्रेजी या हिंदी में उतीर्ण होने की प्रायिकता क्या है?
दो सिक्कों को साथ फेंकने पर, कम से कम एक के पूंछ होने की क्या संभावना है?
एक बॉक्स में, 5 लाल, 9 हरी और 6 काली गेंद हैं । एक गेंद को यादृच्छिक तरीके से से निकाला गया है | इसकी क्या संभावना है कि यह न तो लाल और न ही हरी है?



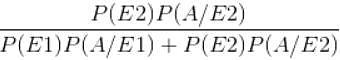 = 8/11
= 8/11














