Test: Probability - 1 - Grade 10 MCQ
10 Questions MCQ Test - Test: Probability - 1
In a bag, there are some red, black and yellow balls. Sum of black and yellow balls is 9. Probability of selecting two red balls from that bag is 1/7 which is 250% of the probability of selecting two black balls. Find number of yellow balls in that bag if the number of black balls is even.
What is the probability of getting more than 5 when dice is trown
A cotton bag B1 has blue pens and red pens in a ratio 3 : 2. Another cotton bag B2 has 7 blue pens, 8 black pens and X green pens. Two pens are drawn from B2 randomly and kept in bag B1. Now a blue pen is drawn from bag B1 such that the probability of drawing a blue pen is 5/9. If (X = Number of blue pens in Bag B1 initially), then what is the total number of pen in bag B1 initially?
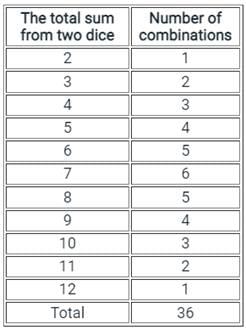
Two unbiased dice are rolled simultaneously. Find the probability of getting sum greater than 5.
A bag contains only red, green and white balls. The probability of selecting a red ball from the bag at random is 1/3 and that of selecting a white ball at random is 1/2. If the bag contains 9 green balls, the total number of balls in the bag is:
Comprehension:
Read the following information and answer the questions given below:
A has 28 elements, B has 32 elements and (A U B) has 40 elements.
How many elements does A ∩ B have?
A dice is thrown. What is the probability that the number shown on the dice is not divisible by 2?
A dice is thrown randomly. What is the probability that the number shown on the dice is not divisible by 3?
From a pack of 52 cards, one black ace, one red king, one black queen and all the four jacks were lost. Find the probability that one card picked out of the remaining cards would be a queen.