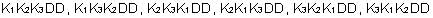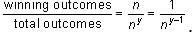Test: Probability- 3 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Probability- 3
A fair coin is flipped three times. What is the probability that the coin lands on heads exactly twice?
There are 10 women and 3 men in room A. One person is picked at random from room A and moved to room B, where there are already 3 women and 5 men. If a single person is then to be picked from room B, what is the probability that a woman will be picked?
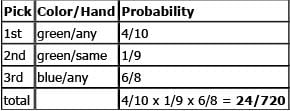
If the probability of rain on any given day in Chicago during the summer i s 50%, independent of what happens on any other day, what is the probability of having exactly 3 rainy days from July 4 through July 8, inclusive?
In a shipment of 20 cars, 3 are found to be defective. If four car s are selected at random, what is the probability that exactly one of the four will be defective?
A certain bag of gemstones is composed of two-thirds diamonds and one-third rubies. If the probability of randomly selecting two diamonds from the bag, without replacement, is 5/12, what is the probability of selecting two rubies from the bag, without replacement?
Triplets Adam, Bruce, and Charlie enter a triathlon. If there are 9 competitors in the triathlon and medals are awarded for first, second, and third place, what is the probability that at least two of the triplets will win a medal?
Set S is the set of all prime integers between 0 and 20. If three numbers are chosen randomly from set S and each number can be chosen only once, what is the positive difference between the probability that the product of these three numbers is a number less than 31 and the probability that the sum of these three numbers is odd?
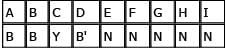
A random 10-letter code is to be formed using the letters A, B, C, D, E, F, G, H, I and I (only the “I” will be used twice). What is the probability that a code that has the two I’s adjacent to one another will be formed?
If p2 – 13p + 40 = q , and p is a positive integer between 1 and 10, inclusive, what is the probability that q < 0?
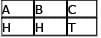
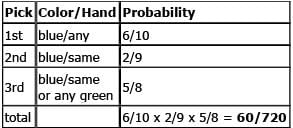
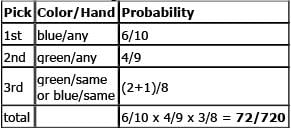
A box cont ains three pairs of blue gloves and two pairs of green gloves. Each pair consists of a left-hand glove and a right-hand glove. Each of the gloves is separate from its mate and thoroughly mixed together with the others in the box. If three gloves are randomly selected from the box, what is the probability that a matched set (i.e., a left- and right-hand glove of the same color) will be among the three gloves selected?
A football team has 99 players. Each pl ayer has a uniform number from 1 to 99 and no two players share the same number. When football practice ends, all the players run off the field one-by-one in a completely random manner. What is the probability that the first four players off the field will leave in order of increasing uniform numbers (e.g., #2, then #6, then #67, then #72, etc)?
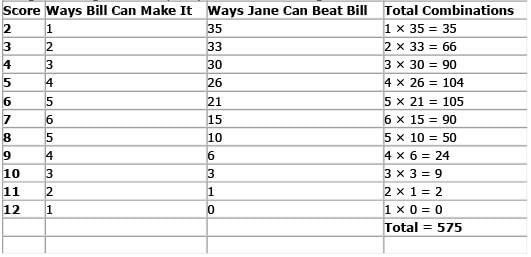
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?
Kate and Danny each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Kate gives Danny $1. Every time the coin lands on tails, Danny gives Kate $1. After the five coin flips, what is the probability that Kate has more than $10 but less than $15?
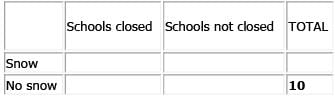
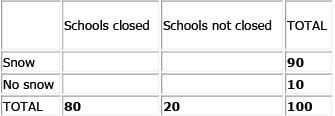
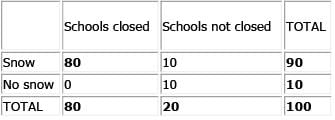
There is a 10% chance that it won’t snow all winter long. There is a 20% chance that schools will not be closed all winter long. What is the greatest possible probability that it will snow and schools will be closed during the winter?
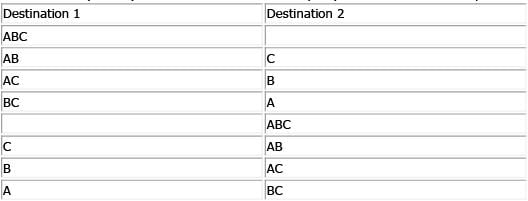
There are y different travelers who each have a choice of vacationing at one of n different destinations. What is the probability that all y travelers will end up vacationing at the same destination?