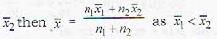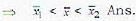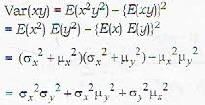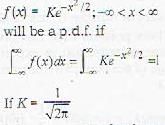Test: Probability and Statistics - 2 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Probability and Statistics - 2
A problem is given to three students A,B and C whose chances of solving it are 1/2 ,1/3 and 1/4 respectively. The probability that this problem will be solved, is :
6 boys and 6 girls sit in a row randomly. The probability that all the girls sit together is :
Probabilities of three students A, B and C to pass an examination arc respectively 1/3,1/4 and 1/5. The probability that exactly one student will pass is :
Different words are written with the letters of PEACE. The probability that both E’s come together is :
The probability of throwing 6 at least one in four throws of a die is :
An untrue coin is such that, when it is tossed the chances of appearing head is twice the chances of appearance of tail. The chance of getting head in one toss of the coin is :
The probability of randomly choosing 3 defectless bulbs from 15 electric bulbs of which 5 bulbs are defective, is :
Probability of four digit numbers, which are divisible by three, formed out of digits 1,2,3,4.5 is :
If X is uniformly distributed over (0, 10), the probability that 1 < X < 6 is
The choice of throwing 12 in a single throw with three dice is
X is a continuous random variable with probability’ function f(x) = N exp(-x2+6x) - ∝ < x < ∝, the value of N is
X is an exponential random variable with parameter λ with p.d.f. (x) = λe-7x if x ≥ 0 = 0 if x < 0, identify the correct one
Determine the value of K for which the function given by f [x, y) = kxy for x = 1, 2, 3 and y = 1,2, 3 can serve as a joint probability distribution
On your way to work, you have to drive through a busy juction where you may be stopped at traffic lights. The cycle of the traffic light is 2 minutes of green followed by 3 minutes of red. What is the expected delay in the journey, if you arrive at the junction at a random time uniformly distributed over the whole 5 minute cycle is?
Let X have the poission distribution with parameter λ such that P(X = k - 1) = r(k) P(X = K). Then r[K] is
If  are the means of two distributions such that
are the means of two distributions such that 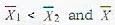 is the mean of the combined distribution, then
is the mean of the combined distribution, then
Suppose that the expected number of accidents per week at an industrial plant is 4. The number of workers injured in each accident is independent random variable with a common mean of 2. Assume also that the number of workers injured in each accident is independent of the number of accidents that occur. The expected number of injuries during a week is
Let X and Y be independent random variables μx and μy and  Then Var (XY) equals
Then Var (XY) equals
f(x) = k, exp 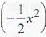 for all x ∈ R; can be a probability density function for
for all x ∈ R; can be a probability density function for
Let x and y be independent random variables with binomial distribution B(10, 1 /3) and B(20, 1/3) respectively. E[x + y] is
|
27 docs|150 tests
|


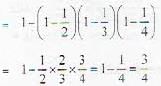
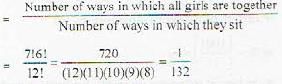

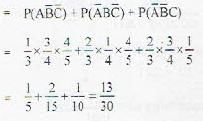
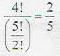
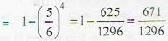

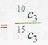

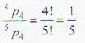
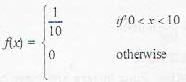
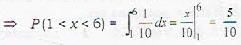


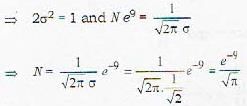

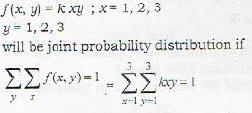
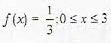
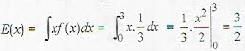
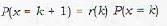
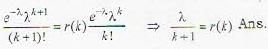
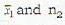 elements has mean
elements has mean