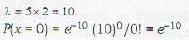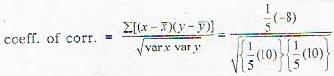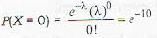Test: Probability and Statistics - 4 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Probability and Statistics - 4
The probability that a number in {1, 2,..., 1001} is divisible by 7 or 11 or both, is
If A and B are two events, the probability that exactly one of them occurs is
A number is chosen from each of the two sets {1 , 2 , 3, 4, 5, 6 , 7. 8 , 9} and {1, 2 . 3, 4, 5, 6 , 7, 8 , 9}. If p1 denotes the probability that the sum of the two numbers be 10 and p2 the probability that their sum be 8, then (p1 + p2] is
The probability that a non-leap year should have 53 Sunday is
A coin is biased so that the probability of head = 1/4. The coin is tossed five times. The probability of obtaining two heads and three tails with heads occurring in succession is
15 coupons are numbered 1,2 ..... 15. Seven coupons are selected at random, one at a time, with replacement. The probability that the largest number appearing on a selected coupon is 9, is
Let A and B be any two arbitrary’ events, then, which of the following is true?
A die is loaded in such a way that each odd number is twice as likely to occur as each even number. If E is the event that a number greater than or equal to 4 occurs on a single toss of the die, then P (E) is
The probability that a person tossing three fair coins will get together all heads or all tails for the second time on the 5th toss is
The probabilities that three men hit a target are 1/6, 1/4, 1/3 respectively. Each shoots once the target. What is the probability that exactly one of them hits the target?
Let X, Y. Z be three independent normal variables N(0, 1). Then E(X - Y + Z)2] is
For a frequency distribution of marks in Mathematics for 100 students, the average was found to be 80. Later on it was discovered that. 4 8 was misread as 84. The correct mean is
For a binomial distribution, the mean is (15/4) and the variance is (15/16). The value of p is
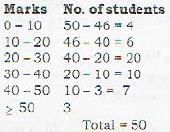
Following is the distribution of marks in Statistics obtained by 50 students :

If 60% of students passes the test, then what is the minimum marks obtained by a candidate who has passed?
Telephone calls come into an exchange according to a Poisson process with 5 calls per minute on the average. The probability that no call will come in during the two minute period 10 A.M. to 10:02 A.M. on a particular day is
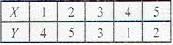
The coefficient of correlation between X and Y for the following bivariate distribution is
X1, X2, .... Xn are independent observations on the random variable X with distribution function F(x). Then the distribution function of Y = Max (X1, X2, ..., Xn) is
Telephone calls come into an exchange according to a Poisson process with 5 calls per minute on the average. The probability that no call will come in during the two-minute period 10 A.M. to 10:02 A.M. on a particular day is
|
27 docs|150 tests
|


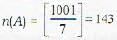
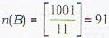
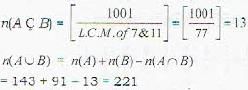

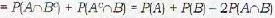

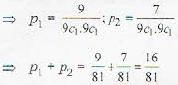

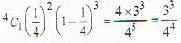
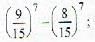 ; as numbers from 1 to 9 is selected 7 times and we subtract the case in which number 1 to 8 is selected all 7 times.
; as numbers from 1 to 9 is selected 7 times and we subtract the case in which number 1 to 8 is selected all 7 times. 
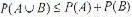


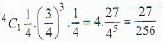
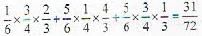
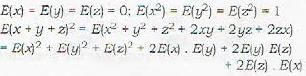
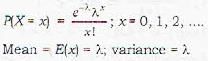
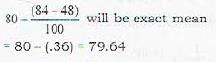
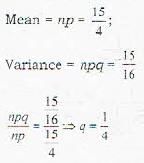
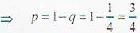
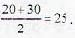 Hence answer is 25.
Hence answer is 25.