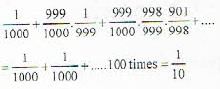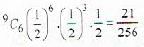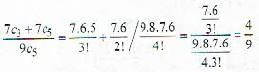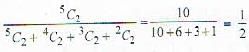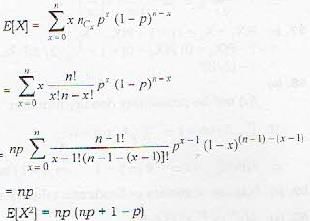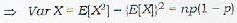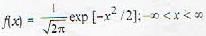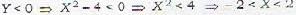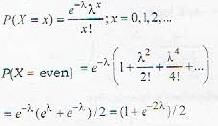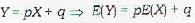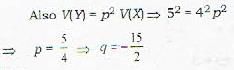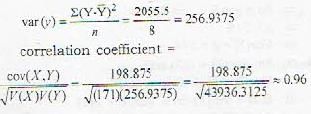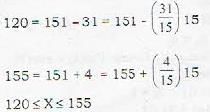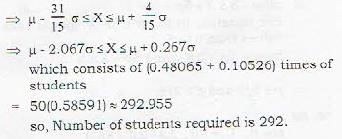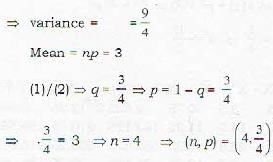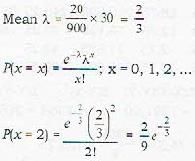Test: Probability and Statistics - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Probability and Statistics - 5
From a pack of 52 cards two are drawn at random. What is the probability that one is a king and the other a queen?
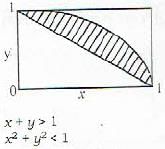
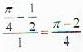
The probability that the sum of two numbers x and y randomly chosen in the interval (0, 1) greater than 1 while the sum of the squares less than 1 is equal to
If the probabilities that A and B will die within a year are p and q respectively, what is the probability that only one of them will be alive at the end of the year?
The probability that a number selected at random between 100 and 999 (both inclusive) will not contain the digit 3 is
At a railway station a passenger leaves his luggage in a locker which is opened by dialling a three-digit code. The passenger chooses the code, closes the locker and leaves for the town. A stranger who does not know the code tries to open the locker by dialling three digits at random without repeating the unsuccessful codes. The probability that the stranger does not have to perform more than 100 trials for a success is
What is the probability of getting seventh head in the tenth toss of an unbiased coin.
A committee of 5 is to be chosen from a group of 9 people. What is the probability that a certain married couple will either serve together or not at all?
What is the probability that the product of two parts of 2n is greater than the 3/4 of their maximum product.
What is the probability that an urn containing 5 balls contains only white balls if the first two balls drawn from it was found to be white
If the probabilities that A and B will die within a year are p and q respectively, then the probability that only one of them will be alive at the end of the year is
It is known that the samples 3.1, 0.2., 1,6, 5.2 and 2.1 are from a random variable that is uniformly distributed over the unknown range (α, β) Find the maximum likelihood estimates for the parameters α and β
We make n independent trials in each of which an event A may occur with probability p. A random variable X is defined as the number of occurrences of the event A in all the n trials. The variance of X is
X is a continuous random variate with pdf  Defining Y = X + 1, E[Y] is found to be
Defining Y = X + 1, E[Y] is found to be
If X is uniformly distributed random variable over the interval (1, 4), the probability V < 0, where Y = X2 - 4 is
Let X be a poisson random variable with parameter λ.P [X is even) is
A teacher on grading an exam finds that the percent marks X have a mean of 62 and a standard deviation of 4. Feeling that the exam may have been unduly difficult, he would like to report a mean of 70 and a standard deviation of 5. He would achieve this by the linear transformation Y = pX + q, where p and q are respectively
What is the correlation coefficient between x and y for the given data :

The mean height of 500 students is 151 cm and the standard deviation is 15 cm. Assuming that the heights are normally distributed, find how many student’s height lie between 120 and 155 cms?
Let X be a binomial random variable with parameters n and p. If the mean and the standard deviation of X are 3 and 3/2, respectively, then what is the value of (n, p)?
Suppose that 20 misprints are distributed randomly in a book of 900 pages. Assuming Poisson distribution, the probability that a chapter of 30 pages contains 2 misprints is
|
27 docs|150 tests
|