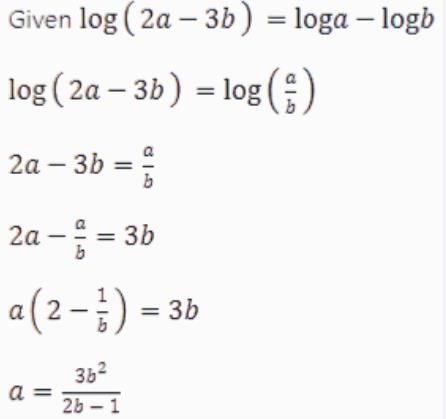Test: Ratio And Proportion, Indices, Logarithms - 1 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Ratio And Proportion, Indices, Logarithms - 1
Choose the most appropriate option.
The inverse ratio of 11 : 15 is
Choose the most appropriate option.
The ratio of two quantities is 3 : 4. If the antecedent is 15, the consequent is
The ratio of the quantities is 5 : 7. If the consequent of its inverse ratio is 5, the antecedent is
The ratio compounded of 2 : 3, 9 : 4, 5 : 6 and 8 : 10 is
The duplicate ratio of 3 : 4 is
The sub duplicate ratio of 25 : 36 is
The ratio compounded of 4:9, and the duplicate ratio of 3:4,the triplicate ratio of 2:3 and 9:7 is
The sub triplicate ratio of 8 : 27 is
The ratio compounded of 4 : 9 and the duplicate ratio of 3 : 4 is
If log (2a - 3b) = log a - log b, then a =
If a : b = 3 : 4, the value of (2a+3b) : (3a+4b) is
Two numbers are in the ratio 2 : 3. If 4 be subtracted from each, they are in the ratio 3 : 5.The numbers are
The angles of a triangle are in ratio 2:7:11. The angles are
Division of Rs. 324 between X and Y is in the ratio 11 : 7. X & Y would get Rupees
The ratio of two numbers is 3 ∶ 2 and the sum of their squares is 468. Find the larger number.
Anand earns Rs.80 in 7 hours and Promod earns Rs.90 in 12 hours. The ratio of their earnings is
The ratio of two numbers is 7 : 10 and their difference is 105. The numbers are
P, Q and R are three cities. The ratio of average temperature between P and Q is 11 : 12 and that between P and R is 9 : 8. The ratio between the average temperature of Q and R is
If x : y = 3 : 4, the value of x2y + xy2 : x3 + y3 is
If p : q is the sub duplicate ratio of p–x2 : q–x2 then x2 is
If 2s : 3t is the duplicate ratio of 2s – p : 3t – p then
If p : q = 2 : 3 and x : y = 4 : 5, then the value of 5px + 3qy : 10px + 4qy is
The number which when subtracted from each of the terms of the ratio 19 : 31 reducing it to 1 : 4 is
Daily earnings of two persons are in the ratio 4:5 and their daily expenses are in the ratio 7 : 9. If each saves Rs. 50 per day, their daily incomes in Rs. are
The ratio between the speeds of two trains is 7 : 8. If the second train runs 400 Kms. in 5 hours, the speed of the first train is
The fourth proportional to 4, 6, 8 is
The third proportional to 12, 18 is
The mean proportional between 25, 81 is
The number which has the same ratio to 26 that 6 has to 13 is
The ratio of the present age of father to that of son is 7:2. After 10 years their ages will be in the ratio of 9:4. The present ages of the father is
|
114 videos|164 docs|98 tests
|