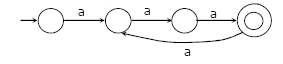Test: Regular Expressions & Finite Automata- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Regular Expressions & Finite Automata- 1
Consider the languages L1 =  and L2 = {a}. Which one of the following represents L1 L2* U L1*
and L2 = {a}. Which one of the following represents L1 L2* U L1*
(A) {∈}
(B) Φ
(C) a*
(D) {∈, a}
(A) {∈}
(B) Φ
(C) a*
(D) {∈, a}
Consider the DFA given.
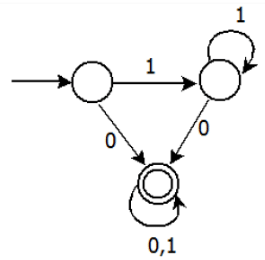
Which of the following are FALSE?
1. Complement of L(A) is context-free.
2. L(A) = L((11*0+0)(0 + 1)*0*1*)
3. For the language accepted by A, A is the minimal DFA.
4. A accepts all strings over {0, 1} of length at least 2.
2. L(A) = L((11*0+0)(0 + 1)*0*1*)
3. For the language accepted by A, A is the minimal DFA.
4. A accepts all strings over {0, 1} of length at least 2.
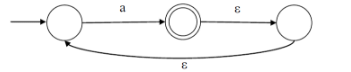
W hat is the complement of the language accepted by the NFA shown below?
Given the language, L = {ab, aa, baa}, which of the following strings are in L*?
1. abaabaaabaa
2. aaaabaaaa
3. baaaaabaaaab
4. baaaaabaa
Consider the set of strings on {0,1} in which, every substring of 3 symbols has at most two zeros. For example, 001110 and 011001 are in the language, but 100010 is not. All strings of length less than 3 are also in the language. A partially completed DFA that accepts this language is shown below
The missing arcs in the DFA are
Definition of a language L with alphabet {a} is given as following.
L={| k>0, and n is a positive integer constant}
Q. What is the minimum number of states needed in DFA to recognize L?
A deterministic finite automation (DFA)D with alphabet {a,b} is given below
Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?
Let w be any string of length n is {0,1}*. Let L be the set of all substrings of w. What is the minimum number of states in a non-deterministic finite automaton that accepts L?
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0+1)*0(0+1)*0(0+1)*?
Which one of the following is FALSE?
Given the following state table of an FSM with two states A and B, one input and one output:
Q. If the initial state is A=0, B=0, what is the minimum length of an input string which will take the machine to the state A=0, B=1 with Output = 1?
Which of the following statements is false?
Given below are two finite state automata (→ indicates the start state and F indicates a final state)Which of the following represents the product automaton Z×Y?
Match the following NFAs with the regular expressions they correspond to:
1. ϵ + 0(01*1 + 00) * 01*
2. ϵ + 0(10 *1 + 00) * 0
3. ϵ + 0(10 *1 + 10) *1
4. ϵ + 0(10 *1 + 10) *10 *
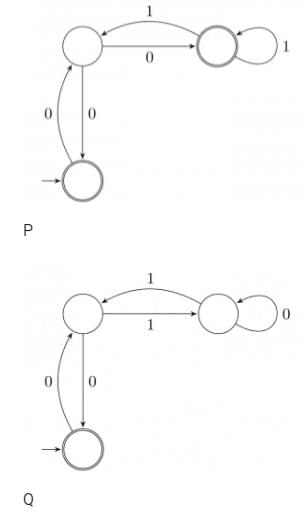
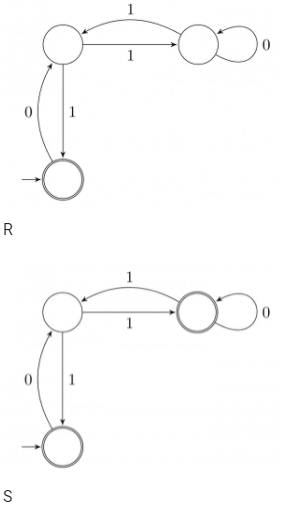
Which of the following are regular sets?
A minimum state deterministic finite automaton accepting the language L={w | w ε {0,1} *, number of 0s and 1s in w are divisible by 3 and 5, respectively} has
Which of the following languages is regular?
Consider the following Finite State Automaton:
The language accepted by this automaton is given by the regular expression
Consider the automata given in previous question. The minimum state automaton equivalent to the above FSA has the following number of states