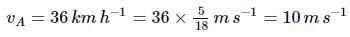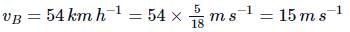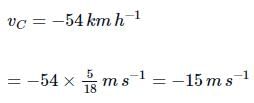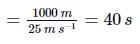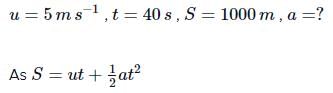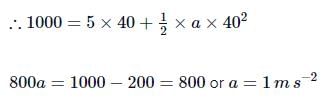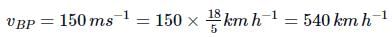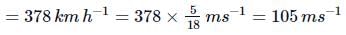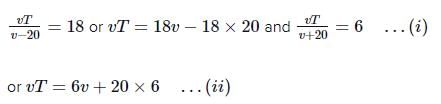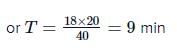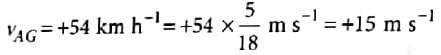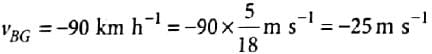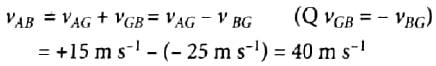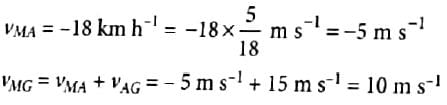Test: Relative Velocity - NEET MCQ
15 Questions MCQ Test - Test: Relative Velocity
A ball A is dropped from a building of height 45 m. Simultaneously another identical ball B is thrown up with a speed 50 m s−1. The relative speed of ball B w.r.t. ball A at any instant of time is (Take g = 10 m s−2).
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed of A relative to B is
Two cars A and B are running at velocities of 60 km h−1 and 45 km h−1. What is the relative velocity of car A with respect to car B, if both are moving eastward?
Two cars A and B are running at velocities of 60 km h−1 and 45 km h−1. What is the relative velocity of car A with respect to car B, if car A is moving eastward and car B is moving westward?
On a two-lane road, car A is travelling with a speed of 36 km h-1. Two cars B and C approach car A in opposite directions with a speed of 54 km h-1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. The minimum required acceleration of car B to avoid an accident is
A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has speed of 27 km h−1 while the other has the speed of 18 km h−1. The bird starts moving from first car towards the other and is moving with the speed of 36 km h−1 when the two were separated by 36 km. The total distance covered by the bird is
A police van moving on a highway with a speed of 30km h−1 fires a bullet at a thief's car speeding away in the same direction with a speed of 192km h−1. If the muzzle speed of the bullet is 150ms−1 , with what relative speed does the bullet hit the thief's car?
A bus is moving with a speed of 10ms−1 on a straight road. A scooterist wishes to overtake the bus in 100s. If the bus is at a distance of 1km from the scooterist with what speed should the scooterist chase the bus?
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 kmh-1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. The period T of the bus service is
A 175m long train is travelling along a straight track with a velocity 72km−1h. A bird is flying parallel to the train in the opposite direction with a velocity 18km−1h. The time taken by the bird to cross the train is
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54kmh−1 and on the other track train B moves south with a speed of 90kmh−1. The velocity of train A with respect to train B is
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54 kmh−1 and on the other track train B moves south with a speed of 90kmh−1. What is the velocity of a monkey running on the roof of the train A against its motion with a velocity of 18 kmh-1 with respect to the train A as observed by a man standing on the ground?
A train A which is 120m long is running with velocity 20m/s while train B which is 130m long is running in opposite direction with velocity 30m/s. What is the time taken by train B to cross the train A?
A jet airplane travelling at the speed of 500kmh−1 ejects its products of combustion at the speed of 1500kmh−1 relative to the jet plane. The speed of the products of combustion with respect to an observer on the ground is
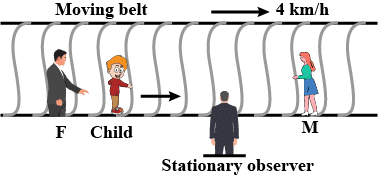
On a long horizontally moving belt, a child runs to and fro with a speed 9kmh−1 (with respect to the belt) between his father and mother located 50m apart on the moving belt. The belt moves with a speed of 4kmh−1. For an observer on a stationary platform, the speed of the child running in the direction of motion of the belt is