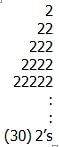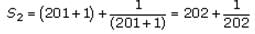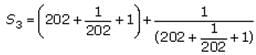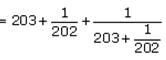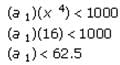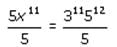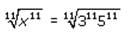Test: Sequences And Series - 1 - Telangana Police Constable MCQ
15 Questions MCQ Test - Test: Sequences And Series - 1
If integer k is equal to the sum of all even multiples of 15 between 295 and 615, what is the greatest prime factor of k?
If S is the infinite sequence S1 = 6, S2 = 12, ..., Sn = Sn-1 + 6,..., what is the sum of all terms in the set {S13, S14, ..., S28}?
In an increasing sequence of 5 consecutive even integers, the sum of the second, third, and fourth integer is 132. What is the sum of the first and last integers?
What is the sum of the multiples of 7 from 84 to 140, inclusive?
If each term in the sum a1 + a2 + a3 + ... +an is either 7 or 77 and the sum is equal to 350, which of the
following could equal to n?
For any integer k from 1 to 10, inclusive, the kth of a certain sequence is given by [(-1)(k+1)] × (1 / 2k). If T is the sum of the first 10 terms of the sequence, then T is:
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?
Sequence S is defined as Sn = 2Sn-1 – 2. If S1 = 3, then S10 – S9 =
Sn = 2Sn-1 + 4 and Qn = 4Qn-1 + 8 for all n > 1. If S5 = Q4 and S7 = 316, what is the first value of n for whichQn is an integer?
What is the sixtieth term in the following sequence? 1, 2, 4, 7, 11, 16, 22...
Sequence S is defined as Sn = X + (1/X), where X = Sn – 1 + 1, for all n > 1.
If S1= 201, then which of the following must be true of Q, the sum of the first 50 terms of S?
In a certain sequence, every term after the first is determined by multiplying the previous term by an integerconstant greater than 1. If the fifth term of the sequence is less than 1000, what is the maximum number ofnonnegative integer values possible for the first term?
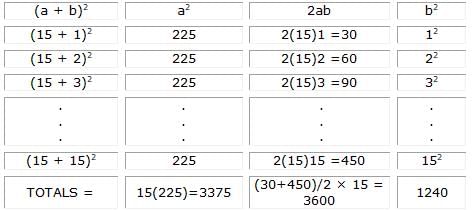
The sum of the squares of the first 15 positive integers (12 + 22 + 32 + . . . + 152) is equal to 1240. What is the sum of the squares of the second 15 positive integers (162 + 172 + 182 + . . . + 302) ?
The infinite sequence Sk is defined as Sk = 10 Sk – 1 + k, for all k > 1. The infinite sequence An is defined as An = 10 An – 1 + (A1 – (n - 1)), for all n > 1. q is the sum of Sk and An. If S1 = 1 and A1 = 9, and if An is positive, what is the maximum value of k + n when the sum of the digits of q is equal to 9?
A certain club has exactly 5 new members at the end of its first week. Every subsequent week, each
of the previous week's new members (and only these members) brings exactly x new members into the club. If y is the number of new members brought into the club during the twelfth week, which of the following could be y?