Test: Sets - 1 - JEE MCQ
25 Questions MCQ Test - Test: Sets - 1
Consider the following statements:
I: If A = {x: x is an even natural number} and B = {y: y is a natural number}, A subset B.
II: Number of subsets for the given set A = {5, 6, 7, 8) is 15.
III: Number of proper subsets for the given set A = {5, 6, 7, 8) is 15.
Which of the following statement(s) is/are correct?
Let A and B be two finite sets having m and n elements, respectively. Then the total number of mapping from A to B is
Consider the following relations:
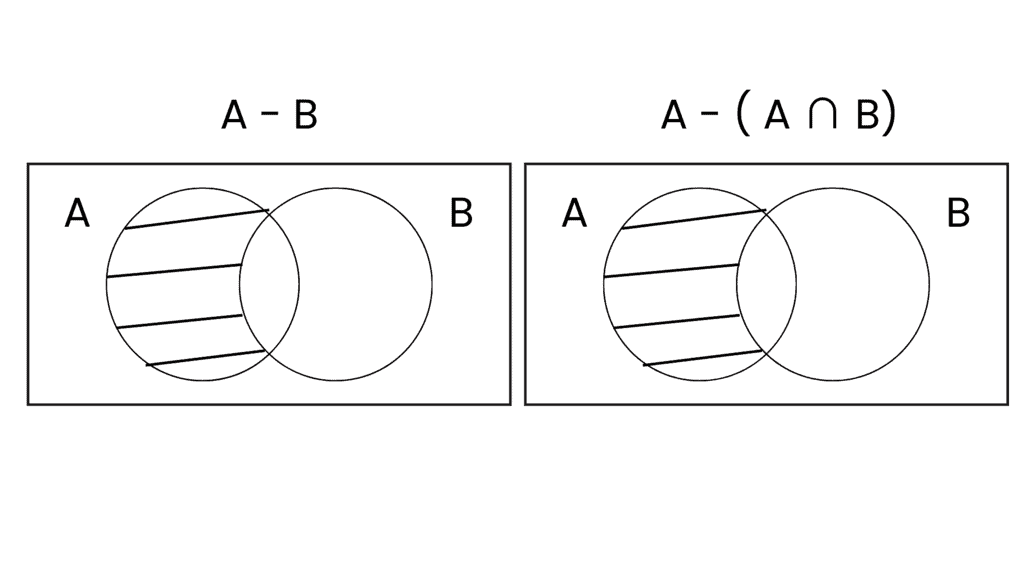
(i) A - B = A - (A ∩ B)
(ii) A = (A ∩ B) ∪ (A - B)
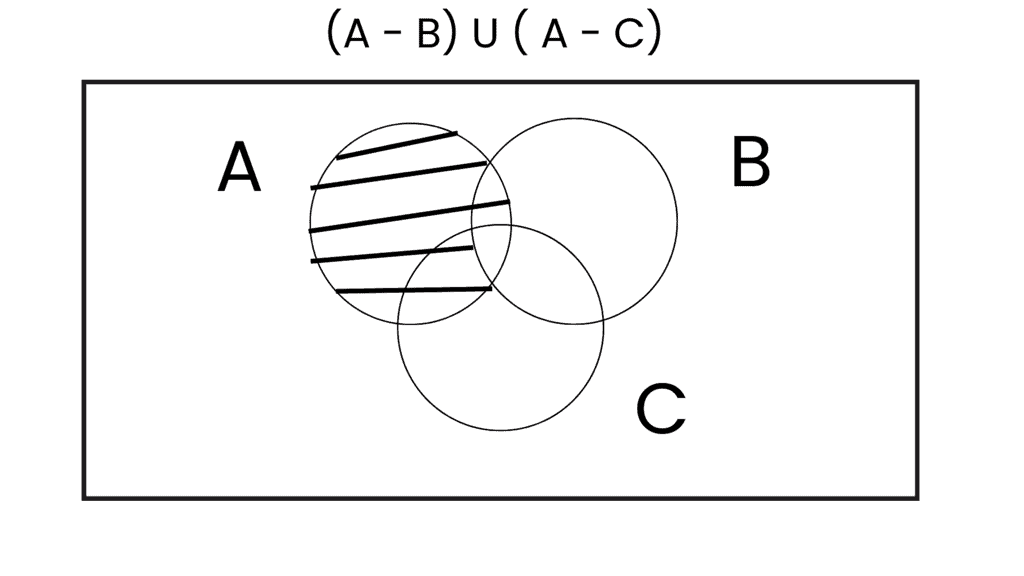
(iii) A - (B ∪ C) = (A - B) ∪ (A - C)
Which of these is/are correct?
(i) A - B = A - (A ∩ B)
(ii) A = (A ∩ B) ∪ (A - B)
(iii) A - (B ∪ C) = (A - B) ∪ (A - C)
Which of these is/are correct?
Two sets, A and B, are as under:
A = {(a, b) ∈ R × R : |a − 5| < 1 and |b − 5| < 1};
B = {a, b) ∈ R × R : 4 (a − 6)2 + 9(b−5) 2 ≤ 36}. Then,
Let A and B be two sets containing 4 and 2 elements, respectively. Then the number of subsets of the set AxB, each having at least 3 elements, is
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 5}, B = {6, 7}. Then A ∩ B’ is:
Which of the following is / are true?
I. If A is a subset of the universal set U, then its complement A′ is also a subset of U.
II. If U = {1,2,3,……,10} and A = {1,3,5, 7,9}, then (A′)′ = A
For a set A, consider the following statements:
1. A ∪ P(A) = P(A)
2. {A} ∩ P(A) = A
3. P(A) − {A} = P(A)
where P denotes power set. Which of the statements given above is/are correct?
If A and B are two disjoint sets, then which one of the following is correct?
Let N denote the set of natural numbers and A={n2 : n ∈ N} and B ={n3 : n ∈ N}. Which one of the following is incorrect?
Let N be the set of non-negative integers, I the set of integers, Np the set of non-positive integers, E the set of even integers and P the set of prime numbers. Then
A,B,C and D are four sets such that A ∩ B = C ∩ D = ϕ. Consider the following:
1. A ∪ C and B ∪ D are always disjoint.
2. A ∩ C and B ∩ D are always disjoint Which of the above statements is/are correct?
Let A,B,C are three non-empty sets. If A ⊂ B and B ⊂ C, then which of the following is true?
Let X and Y be two non-empty sets such that X ∩ A = Y ∩ A = ϕ and X ∪ A = Y ∪ A for some non-empty set A. Then
Which one of the following is correct? Here P(A) denotes the power set of a set A.
If (A − B) ∪ (B − A) = A for subsets A and B of the universal set U, then which one of the following is correct?
Let n(U) = 700,n(A) = 200,n(B) = 300,n(A ∩ B) = 100, then n( A′ ∩ B′) is equal to
The number of elements in the set { n ∈ Z : |n² – 10n + 19| < 6 } is