Test: Solid Mechanics
25 Questions MCQ Test GATE Civil Engineering (CE) 2023 Mock Test Series | Test: Solid Mechanics
| 1 Crore+ students have signed up on EduRev. Have you? |
According to Euler's column theory, the crippling load of a column is given by p = π2 EI/Cl2 In this equation, the value of C for a column with both ends hinged, is
In the formula l is the critical length. If both the end is fixed l= l/2 if both the end is hanged l= l if one end is fixed and other is hinged l= l/root2 if one end fixed other is free l= 2l Hence, in your question, option c is right.
A strut 2.5m long is 60mm in diameter. One end of the strut is fixed while its other end is hinged. Using factor of safety 3.5, the safe compressive load for the member is:
E = 2.1 × 105 N/mm2
E = 2.1 × 105 N/mm2
Step 1: Data
Length of the column = 2500mm
Diameter of the column = 60mm
Condition = one end hinged and other end fixed
Crippling load =??
FOS=3.5
E=2.1x105N/mm2
Step 2: Calculation of moment of inertia
I = π d 4 / 64
I= π (60)4 / 64
I = 0.636X106mm4
Step 3: Calculation of crippling load
Condition = one end hinged and other end fixed
P = 2 Π 2E I/ L2
P = 2 Π 2(2.1x105) (0.636X106) / (2500)2
P = 421.81 KN
Step 4: Calculation of safe load
Safe load = crippling load /FOS
Safe load = 421.81/3.5
Safe load = 120.52KN
Figure shows a slender bar of area A and length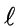 
pinned to immovable supports. Rise in temperature required to produce buckling of bar is
pinned to immovable supports. Rise in temperature required to produce buckling of bar is
A solid circular compression member 50mm in diameter is to be replaced by a hollow circular section of the same material. Find the size of hollow section if internal diameter is 0.6 times external diameter.
A hollow alloy tube 5m with external and internal diameters equal to 40mm and 25mm respectively was found to extend by 6.4mm under a tensile load of 60kN. When tube is used as column with both ends pinned, find safe compressive load for tube. (FOS = 4)
Young's modulus is a measure of the stiffness of an elastic material, and it is defined as the ratio of stress to strain. Rocks with low Young's modulus tend to be ductile and rocks with high Young's modulus tend to be brittle.
Hollow C.I. column whose outside diameter is 200mm has thickness of 20mm. It is 7.5m long and is fixed at both ends. Find the ratio of Euler’s and Rankine’s critical loads. For C.I., σc = 550N/mm2, α = 1/1600, E = 8 × 104 N/mm2
Common data for 8 & 9
Beam 8m long fixed at both ends carries a UDL over whole span. Take EI = 9.5 × 109 kNmm. Find load intensity on beam:-
Q. When maximum Bending Moment should not exceed 40 kN-m.
Common data for 8 & 9
Beam 8m long fixed at both ends carries a UDL over whole span. Take EI = 9.5 × 109 kNmm. Find load intensity on beam:-
Q. When maximum deflection should not exceed 1/400 of the span.
Max deflection =(1/400)×8000 => 20mm. For fixed beam with entire UDL ,Max deflection = wl'4/(384EI)= (20×384× 9.5×10'9)/(8000)'4 => 0.0178 KN /mm => 17.8 KN/m
Vessel in the shape of spherical shell 800mm in diameter, 10mm shell thickness is completely filled with a fluid at atmospheric pressure. Additional fluid is then pumped in till pressure increases by 5 N/mm2. Find volume of this additional fluid.
μ= 0.25, E = 2 × 105 N/mm2
A solid shaft of 200mm diameter has the same cross-sectional area as that of hollow shaft of same material with inside diameter of 150mm. Find ratio of power transmitted by two shafts at same speed.
A hollow shaft is to transmit 300kW at 80rpm. If shear stress is not to exceed 60 N/mm2 and internal diameter is 0.6 of the external diameter, find external and internal diameters assuming maximum torque is 1.4 times the
mean torque.
A cast iron test beam 20mm × 20mm in section and 1m long and supported at the end fails when a central load of 640 N is applied.
What uniformily distributed load will break a cantilever of the same material 50mm wide, 100mm deep and 2m long?
An I-section beam as shown, is simply supported over a span of 10m. If the maximum permissible bending stress is 80 N/mm2. What concentrated load can be carried at a distance of 3.5m from one support.
A 3m high pole stands as a vertical cantilever fixed at its base. It has to support a horizontal load of 10kN at its top. Find the minimum diameter required if the pole is of wood, if the permissible bending stress is 15N/mm2
A steel beam of solid circular section 25mm in diameter and length 1m is simply supported at both ends, and is loaded by its own weight only. If steel weights at 77000 N/m3, what is the length of the beam at which it just starts yeilding. Take Yeild stress = 207N/mm2
Two planes AB and BC which are at right angles carry shear stresses of intensity 17.5 N/mm2 while these
planes also carry tensile stress of 70 N/mm2 and compressive stress of 35N/mm2 respectively. Position of
principal planes is given as:-
Consider 2 - D state of stress as shown:-
Coordinates of centre of Mohr’s circle is:-
At a point in a 2D stress system, σx = 100 N/mm2 , σy =τxy 40 N/mm2. What is the radius of Mohr’s circle
for stress drawn with scale 1cm = 10 N/mm2 ?
A steel bar 15mm in diameter is pulled axially by a force of 10 kN. If the bar is 250mm long, calculate the strain energy per unit volume stored by bar in (N-mm/mm3)
(Esteel = 2 × 105 N/mm2)
Rod with coefficient of linear expansion 0.000012 per oC and E = 1 × 105 N/mm2 is 2m long at 10 oC. Expansion of rod when temperature is raised to 800C is :-
Brass rod 20mm in diameter is subjected to tensile load of 40 kN. Extension of rod measured with extension meter is found to be 254 divisions in 200mm. If each division is equal to 0.001mm, the elastic modulus of brass is :-
The bend ABC shown in the figure carries a concentrated vertical load P at A. The horizontal deflection at A is
[Assume uniform flexural rigidity]
Differentiating strain energy w.r.t Q will give horizontal deflection of A
For the frame shown in the figure, find the horizontal deflection of the roller end D
Consider a beam with circular cross-section of diameter d. The ratio of the second moment of area about the neutral axis to the section modulus of the area is
For circular cross-section,
Second moment of area of beam –πd4/64
section modulus = πd3/32
dividing ( I ) and (2),
we get
:. Ratio = d /2
|
26 docs|292 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
26 docs|292 tests
|
Download free EduRev App
Related content with Test: Solid Mechanics
|
|
|
|
Related tests with Test: Solid Mechanics
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
