Test: Spanning Tree - Computer Science Engineering (CSE) MCQ
24 Questions MCQ Test - Test: Spanning Tree
Let G be a weighted connected undirected graph with distinct positive edge weights. If every edge weight is increased by the same value, then which of the following statements is/are TRUE?
P: Minimum spanning tree of does not change.
Q: Shortest path between any pair of vertices does not change.
Q: Shortest path between any pair of vertices does not change.
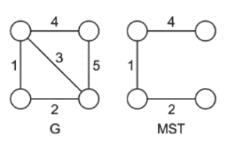
 is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G . Whichof the following statements about the minimum spanning trees
is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G . Whichof the following statements about the minimum spanning trees 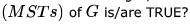
I. If e is the lightest edge of some cycle in G, then every MST of G includes .
II. If e is the heaviest edge of some cycle in G, then every MST of G excludes e .
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only:
Kruskal’s algorithm for finding a minimum spanning tree of a weighted graph G with n vertices and edges has the time complexity of:
Let G be an undirected connected graph with distinct edge weights. Let emax be the edge with maximum weight and the edge with minimum weight. Which of the following statements is false?
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
Consider a weighted complete graph G on the vertex set {v1,v2,.....vn} such that the weight of the edge (vi, vj) is . The weight of a minimum spanning tree of G is:
Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry Wij in the matrix W below is the weight of the edge {i, j}.
In the graph given in above question, what is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges?
Let ω be the minimum weight among all edge weights in an undirected connected graph. Let e be a specific edge of weight ω . Which of the following is FALSE?
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree?
Consider the following graph:
Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm?
Consider a complete undirected graph with vertex set
What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?
An undirected graph G (V,E) contains n(n>2) nodes named v1,v2,.......vn. Two nodes vi,vj are connected if and only if Each edge (vi,vj) is assigned a weight i=+j. A sample graph with n=4 is shown below.
What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?
Consider a complete undirected graph with vertex set Entry Wij in the matrix W below is the weight of the edge
What is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges?
Let G be a weighted graph with edge weights greater than one and G' be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'. Which of the following statements is TRUE?
Let G be a connected simple graph (no self-loops or parallel edges) on n ≥ 3vertices, with distinct edge weights. Let e1,e2........em be an ordering of the edges in decreasing order of weight. Which of the following statements is FALSE?
In a connected weighted graph with vertices, all the edges have distinct positive integer weights. Then, the maximum number of minimum weight spanning trees in the graph is
Consider the following undirected connected graph G with weights on its edges as given in the figure below. A minimum spanning tree is a spanning tree of least weight and a maximum spanning tree is one with largest weight. A second best minimum spanning tree whose weight is the smallest among all spanning trees that are not minimum spanning trees in G.
Which of the following statements is TRUE in the above graph? (Note that all the edge weights are distinct in the above graph)
Let be a connected undirected graph of 100 vertices and 300 edges. The weight of a minimum spanning tree of is 500. When the weight of each edge of is increased by five, the weight of a minimum spanning tree becomes ______.
The graph shown below has 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is_______________.
The number of distinct minimum spanning trees for the weighted graph below is _____
How many minimum spanning trees does the following graph have? Draw them. (Weights are assigned to edges).
An undirected graph G(V, E) contains n ( n > 2 ) nodes named v1 , v2 ,….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| <= 2. Each edge (vi, vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below.
The length of the path from v5 to v6 in the MST of previous question with n = 10 is
Let G be a complete undirected graph on 4 vertices, having 6 edges with weights being 1, 2, 3, 4, 5, and 6. The maximum possible weight that a minimum weight spanning tree of G can have is __________