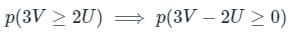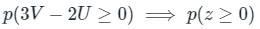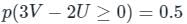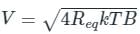Test: Special Classes of Random Processes - Electronics and Communication Engineering (ECE) MCQ
8 Questions MCQ Test Communication System - Test: Special Classes of Random Processes
Let U and V be two independent zero mean Gaussian random variables of variances 1/4 and 1/9 respectively. The probability P(3V ≥ 2U) is
A device has 200 Ω equivalent noise resistance, 300 Ω input resistor, and the bandwidth of the amplifier is 6 MHz. If the operating temperature of the amplifier is 290° K, the noise voltage at the input of a television RF amplifier will be nearly
Which method is much better and efficient?
Which reduces the dynamic range of quantization noise in PCM?
Air craft of Jet Airways at Ahmedabad airport arrive according to a Poisson process at a rate of 12 per hour. All aircraft are handled by one air traffic controller. If the controller takes a 2 – minute coffee break, what is the probability that he will miss one or more arriving aircraft?
A random process is defined by X(t) + A where A is continuous random variable uniformly distributed on (0,1). The auto correlation function and mean of the process is
The auto correlation function of a stationary ergodic random process is shown below.
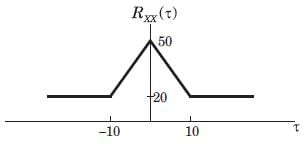
What is the value of variance?
|
13 videos|39 docs|30 tests
|