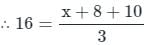Test: Statistics - 1 - UPSC MCQ
20 Questions MCQ Test - Test: Statistics - 1
The extreme values in negatively skewed distribution lie in the_____.
Let the average of three numbers be 16. If two of the numbers are 8 and 10, what is the remaining number?
The appropriate average for calculating average percentage increase in population is____________.
If the mode of the following data is 7, then the value of k in the data set 3, 8, 6, 7, 1, 6, 10, 6, 7, 2k + 5, 9, 7, and 13 is:
The measures of dispersion are changed by the change of__________.
If mean and mode of some data are 4 & 10 respectively, its median will be:
A set of values is said to be relatively uniform if it has_______.
What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
A symmetrical distribution has mean equal to 4. Its mode will be______.
If mean is less than mode, the distribution will be__________.
The observations 4, 1, 4, 3, 6, 2, 1, 3, 4, 5, 1, 6 are outputs of 12 dices thrown simultaneously. If m and M are means of lowest 8 observations and highest 4 observations respectively, then what is (2m + M) equal to?
The distribution in which mean = 60 and mode = 50, will be ________
Which among the following are the measures of Central Tendency or Measures of Location?
A. Mean
B. Range
C. Mode
D. Median
E. Variance
Choose the most appropriate answer from the options given below:
If the mean of 5 observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the mean of last 3 observations is