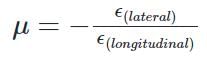Test: Stress & Strain - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Stress & Strain - 1
If a body is stressed within its elastic limit, the lateral strain bears a constant ratio to the linear strain. This constant is known as:
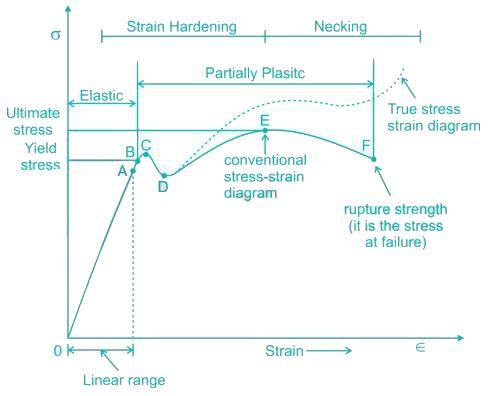
Which point on the stress strain curve occurs after proportionality limit?
A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?
A static load is mounted at the centre of a shaft rotating at uniform angular velocity. This shaft will be designed for
Which of the following is a good example of a composite bar?
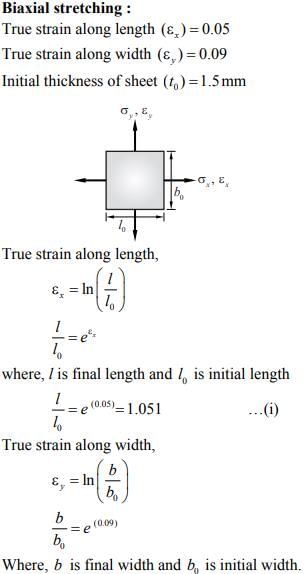
A 1.5 mm thick sheet is subject to unequal biaxial stretching and the true strains in the directions of stretching are 0.05 and 0.09. The final thickness of the sheet in mm is
A steel bar of 40 mm × 40 mm square cross-section is subjected to an axial compressive load of 200 kN. If the length of the bar is 2 m and E = 200 GPa, the elongation of the bar will be:
The ultimate tensile strength of a material is 400 MPa and the elongation up to maximum load is 35%. If the material obeys power law of hardening, then the true stress-true strain relation (stress in MPa) in the plastic deformation range is:
An axial residual compressive stress due to a manufacturing process is present on the outer surface of a rotating shaft subjected to bending. Under a given bending load, the fatigue life of the shaft in the presence of the residual compressive stress is:
A test specimen is stressed slightly beyond the yield point and then unloaded. Its yield strength will
The deformation of a bar under its own weight as compared to that when subjected to a direct axial load equal to its own weight will be:
The phenomenon of slow growth of strain under a steady stress is called:
A bar of length L tapers uniformly from diameter 1.1 D at one end to 0.9 D at the other end. The elongation due to axial pull is computed using mean diameter D. What is the approximate error in computed elongation?
In the case of an engineering material under unidirectional stress in the x -direction, the Poisson's ratio is equal to (symbols have the usual meanings)
If a piece of material neither expands nor contracts in volume when subjected to stress, then the Poisson‟s ratio must be
Assertion (A): Plastic deformation is a function of applied stress, temperature and strain rate.
Reason (R): Plastic deformation is accompanied by change in both the internal and external state of the material.
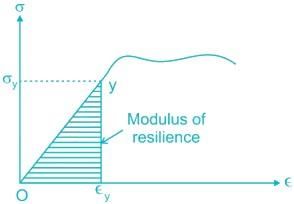
The maximum energy that can be absorbed up to the elastic limit, without creating a permanent distortion is called
Consider the following statements regarding the principle of super position:
1. The total displacement of the stress at a point in a structure subjected to several external loadings can be determined by adding together the displacements caused by each of the external loads acting together.
2. The material must behave in a non-linear elastic manner.
3. The geometry of the structure must not undergo significant change when the loads are applied.
Which of the above statements is/are correct?
If the value of Poisson's ratio is zero, then it means that
Engineering strain of a mild steel sample is recorded as 0.100%. The true strain is