Test: Systems of Linear Equations, Matrix Algebra & Transform Theory- 1 - Civil Engineering (CE) MCQ
20 Questions MCQ Test - Test: Systems of Linear Equations, Matrix Algebra & Transform Theory- 1
The system of linear equations
4x + 2y = 7
2x + y = 6 has
4x + 2y = 7
2x + y = 6 has
For the following set of simultaneous equations:
1.5x – 0.5y = 2
4x + 2y + 3z = 9
7x + y + 5z = 10
1.5x – 0.5y = 2
4x + 2y + 3z = 9
7x + y + 5z = 10
The following set of equations has
3 x + 2 y + z = 4
x – y + z = 2
-2 x + 2 z = 5
3 x + 2 y + z = 4
x – y + z = 2
-2 x + 2 z = 5
Consider the system of simultaneous equations
x + 2y + z = 6
2x + y + 2z = 6
x + y + z = 5
This system has
Multiplication of matrices E and F is G. Matrices E and G are
What is the matrix F?
Consider a non-homogeneous system of linear equations representing mathematically an over-determined system. Such a system will be
For the set of equations
x1 + 2x + x3 + 4x4 = 0
3x1 + 6x2 + 3x3 + 12x4 = 0
Let P ≠ 0 be a 3 × 3 real matrix. There exist linearly independent vectors x and y such that Px = 0 and Py = 0. The dimension of the range space of P is
The eigen values of a skew-symmetric matrix are
The rank of a 3×3 matrix C (=AB), found by multiplying a non-zero column matrix Aof size 3×1 and a non-zero row matrix B of size 1×3, is
Match the items in columns I and II.
Column I Column II
P. Singular matrix 1. Determinant is not defined
Q. Non-square matrix 2. Determinant is always one
R. Real symmetric 3. Determinant is zero
S. Orthogonal matrix 4. Eigenvalues are always real
5. Eigenvalues are not defined
Real matrices are given. Matrices [B] and
[E] are symmetric.
Following statements are made with respect to these matrices.
1. Matrix product [F]T [C]T [B] [C] [F] is a scalar.
2. Matrix product [D]T [F] [D] is always symmetric.
With reference to above statements, which of the following applies?
The product of matrices (PQ)–1 P is
The matrix A
=
is decomposed into a product of a lower triangular matrix [L] and an upper triangular matrix [U]. The properly decomposed [L] and [U] matrices respectively are
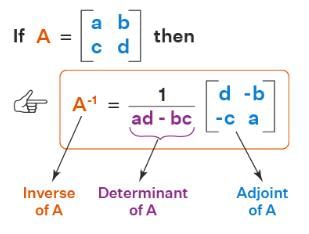
The inverse of the matrix is
The inverse of the 2 × 2 matrix is,
For what value of λ, do the simultaneous equation 2x + 3y = 1, 4x + 6y = λ have infinite solutions?
Consider the following system of linear equations:x + 2y + z = 32x + 4y + 2z = 63x + 6y + 3z = 9What is the solution for the system?
The system of equations
x + y + z = 6;
x + 4y + 6z = 20;
x + 4y + λz = μ
has NO solution for values of λ and μ given by
Real matrices are given. Matrices [A] and [B] are symmetric.Following statements are made with respect to these matrices:The matrix product [X]T [A]T [B] [A] [X] is a scalar.The matrix product [Y]T [X] [Y] is always symmetric.With reference to the above statements, which of the following applies?



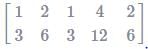







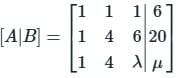
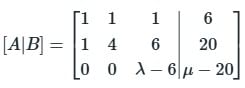 …
…










