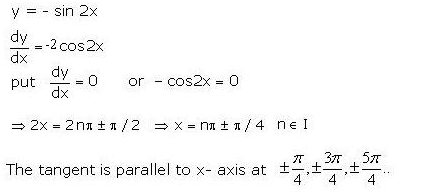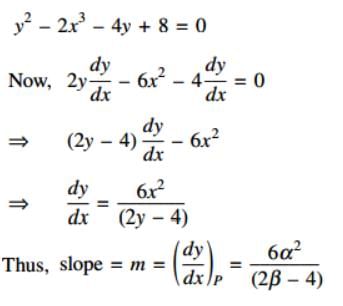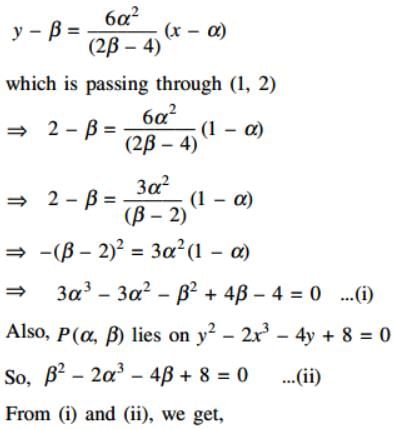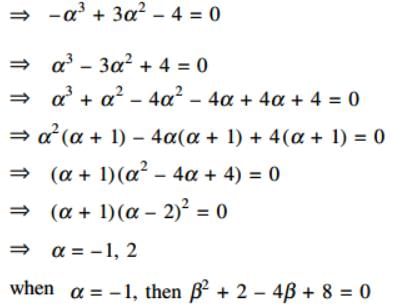Test: Tangents And Normals - JEE MCQ
10 Questions MCQ Test - Test: Tangents And Normals
Find slope of normal to the curve y=5x2-10x + 7 at x=1
The equation of the tangent line to the curve y = 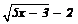 which is parallel to the line 4x -2y + 3 = 0 is
which is parallel to the line 4x -2y + 3 = 0 is
If y = – sin2x. Find the values of x at which the tangents drawn to the graph of this function is parallel to the x- axis.
The normal at any point q to the curve x = a (cos q + q sin q), y = a (sin q – q cos q) is at distance from the origin that is equal to… .
The equation of the normal to the curve x2 = 4y which passes through the point (1, 2) is.
The curve y = ax3 + bx2 + cx + 5 touches the x-axis at P(-2, 0) and cuts the y-axis at the point Q where its gradient is 3. the equation of the curve is… .
If a, b are real numbers such that x3-ax2 + bx – 6 = 0 has its roots real and positive then minimum value of b is
The equation of tangent to the curve y = x3 + 2x + 6 which is perpendicular to the line x + 14y + 4 = 0 is :
The equations of the tangents drawn to the curve y2 – 2x3 – 4y + 8 = 0 from the point (1, 2) is… .