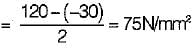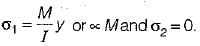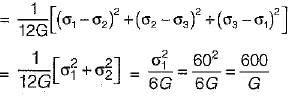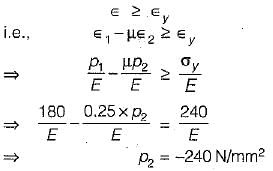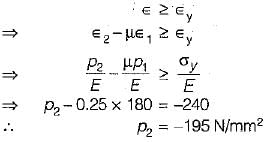Test: Theories of Failure
10 Questions MCQ Test GATE Civil Engineering (CE) 2023 Mock Test Series | Test: Theories of Failure
| 1 Crore+ students have signed up on EduRev. Have you? |
A certain steel has proportionality limit of 300 N/mm2 in simple tension. It is subjected to principal stress of 120 N/mm2 (tensile), 60 N/mm2 (tensile) and 30 N/mm2 (compressive). The factor of safety according to maximum shear stress theory is
Proportionality limit shear stress
= 300/2 = 150N/mm2
Maximum shear stress
∴ Factor of safety = 150/75 = 2.0
All the theories of failure, will give nearly the same result when
When one of the principal stresses at a point is large in comparison to the other, the situation resembles uniaxial tension test. Therefore all theories give nearly the same results.
The principal stresses developed at a point are +60, -60, 0 MPa. Using shear strain energy theory, factor of safety obtained is √3. What is yield stress of the material?
The yield stress of a material is the maximum stress that a material can withstand before it begins to yield or deform plastically. The yield stress is often determined using the shear strain energy theory, which states that the yield stress is equal to the product of the factor of safety and the maximum principal stress.
In this case, the maximum principal stress is 60 MPa and the factor of safety is √3.
Therefore, the yield stress of the material is 60 MPa * √3 = 180 MPa.
Therefore, the correct answer is D.
For ductile material the most suitable theory is maximum shear stress theory.
Other theories for ductile material, Maximum Strain Energy Theory and Maximum Shear Stress Theory (Most Conservative Theory)
For brittle material the most suitable theory is Maximum Principal Stress Theory.
Other theories for brittle material, Maximum Principal Stress Theory.
Which of the following theories of failure is most appropriate for a brittle material?
Maximum principal stress theory (Rankine theory) is suitable for brittle materials.
In a structural member, there are perpendicular tensile stresses of 100 N/mm2 and 50 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0.25)
Equivalent stress
= σ1 - μσ2
= 100 - 0.25 x 50 = 87.5 N/mm2
Permissible bending moment in a circular shaft under pure bending is M, according to maximum principal stress theory of failure. According to maximum shear theory of failure, the permissible bending moment in the shaft is
According to maximum principal stress theory,
σ1 = σy
According to maximum shear stress theory,
σ1 - σ2 = σy
Under pure bending, 
Therefore, in both the cases, permissible bending moment is M,
A shaft subjected to pure torsion is to be designed which of the following theories gives the largest diameter of shaft?
It is clear from the relation T/J = (Shear Stress)/ (Radial Distance) that a shaft subjected to pure torsion is to be designed for maximum shear stress theory.
If maximum principal stress σ1 = 60 N/mm2, σ2 and σ3 of value zero act on a cube of unit dimensions, then the maximum shear stress energy stored in it would be
Shear strain energy
In a 2D stress system, the two principal stress are p1 = 180 N/mm2 (tensile) and p2 (compressive). For the materials, yield stress in simple tension and compression is 240 N/mm2 and Poisson’s ratio is 0.25. According to maximum normal strain theory for what value of p2 shall yielding commence?
Yielding may occur either in tension or compression.
For yielding in tension,
According to normal strain theory,
For yielding in compression,
|
27 docs|296 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
27 docs|296 tests
|
Download free EduRev App
Related content with Test: Theories of Failure
|
|
|
|
Related tests with Test: Theories of Failure
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
