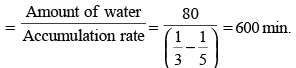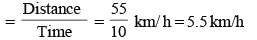Test: Time, Distance & Work - CAT MCQ
30 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Time, Distance & Work
One can use three different transports which move at 10, 20, and 30 kmph, respectively. To reach from A to B, Amal took each mode of transport 1/3 of his total journey time, while Bimal took each mode of transport 1/3 of the total distance. The percentage by which Bimal’s travel time exceeds Amal’s travel time is nearest to
(2019)
Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is
(2019)
In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse?
(2019)
The wheels of bicycles A and B have radii 30 cm and 40 cm, respectively. While traveling a certain distance, each wheel of A required 5000 more revolutions than each wheel of B. If bicycle B traveled this distance in 45 minutes, then its speed, in km per hour, was
(2019)
At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency?
(2019)
Three men and eight machines can finish a job in half the time taken by three machines and eight men to finish the same job. If two machines can finish the job in 13 days, then how many men can finish the job in 13 days?
(2019)
John jogs on track A at 6 kmph and Mary jogs on track B at 7.5 kmph. The total length of tracks A and B is 325 metres. While John makes 9 rounds of track A, Mary makes 5 rounds of track B. In how many seconds will Mary make one round of track A?
(2019)
Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job. If Bimal has done 10% of the job, then in how many days was the job done?
(2019)
A cyclist leaves A at 10 am and reaches B at 11 am. Starting from 10:01 am, every minute a motor cycle leaves A and moves towards B. Forty-five such motor cycles reach B by 11 am. All motor cycles have the same speed. If the cyclist had doubled his speed, how many motor cycles would have reached B by the time the cyclist reached B?
(2019)
Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anticlockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at
(2019)
John gets ₹ 57 per hour of regular work and ₹ 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
(2019)
Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it?
(2018)
A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on?
(2018)
When they work alone, B needs 25% more time to finish a job than A does. They two finish the job in 13 days in the following manner: A works alone till half the job is done, then A and B work together for four days, and finally B works alone to complete the remaining 5% of the job. In how many days can B alone finish the entire job?
(2018)
Point P lies between points A and B such that the length of BP is thrice that of AP. Car 1 starts from A and moves towards B. Simultaneously, car 2 starts from B and moves towards A. Car 2 reaches P one hour after car 1 reaches P. If the speed of car 2 is half that of car 1, then the time, in minutes, taken by car 1 in reaching P from A is
(2018)
Train T leaves station X for station Y at 3 pm. Train S, traveling at three quarters of the speed of T, leaves Y for X at 4 pm. The two trains pass each other at a station Z, where the distance between X and Z is three-fifths of that between X and Y. How many hours does train T take for its journey from X to Y?
(2018)
The distance from A to B is 60 km. Partha and Narayan start from A at the same time and move towards B. Partha takes four hours more than Narayan to reach B. Moreover, Partha reaches the mid-point of A and B two hours before Narayan reaches B. The speed of Partha, in km per hour, is
(2018)
A man travels by a motor boat down a river to his office and back. With the speed of the river unchanged, if he doubles the speed of his motor boat, then his total travel time gets reduced by 75%. The ratio of the original speed of the motor boat to the speed of the river is
(2017)
There are three cities A, B and C, not on the same straight road. Two buses P and Q start simultaneously from A and B respectively towards C. By the time Q reaches C, P is exactly halfway to C. Immediately after Q reaches C, it starts travelling towards A and it crosses P at a point 165 km from A. The ratio of the speeds of P and Q is 3 : 5 Assume that the roads joining A to C, B to C and B to A are all straight roads. If B is twice as far from A as it is from C and P would take to cover the distance from A to B, how much time would Q take to cover the distance from C to A?
(2016)
There is a string of length 100 m running from east to west. 1000 ants are dropped onto the string. Assume that each ant lands on the string facing either the east or the west direction. As soon as they land, each ant starts moving in the direction which is being faced by it at 50 m/ min till it falls off the string. But if an ant collides with another ant coming from the opposite direction, both of them reverse their directions and proceed to move now in the opposite directions. Ants fall only at either of the ends of the string. What is the minimum time by which the string is definitely free of ants?
(2015)
P, Q and R start walking from the same point. P and Q start at 1 PM and R starts at 3 PM. R takes over P at 5 PM and then doubles his speed and takes over Q after another hour. What is the ratio of speed of A and speed of B?
(2014)
Once upon a time, the king of a jungle planned a 2-kilometre race between a rabbit and a tortoise. Soon after the start of the race, the rabbit took a huge lead. On realizing that even after taking a nap of ‘t’ min, he would beat the tortoise by 13 min, he stooped under a tree and went to sleep. Meanwhile the tortoise kept walking. When the rabbit woke up, he realized that he had slept for (14 + t) min, and immediately started running towards the target at a speed 3/2 times his original speed. The race eventually ended in a dead heat. If the ratio of the original speed of the rabbit to that of the tortoise was 6 : 1 and the rabbit overstretched his nap by 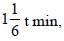 then how long did the tortoise take to complete the race?
then how long did the tortoise take to complete the race?
(2013)
Anushka and Anirudh working together can complete a piece of work in 20 days. They started the work together, but Anushka left after x days and Anirudh finished the remaining work in the next x/2 days. Had Anushka left after 3x/4 days, Anirudh would have taken x days to finish the remaining work. Find the ratio of the efficiency of Anushka to that of Anirudh.
(2013)
During his trip to England, Mr. Clockilal, a horologist, decided to visit ‘The Cuckooland Museum’ dedicated to the exhibition of cuckoo clocks. He entered the museum between 12 noon and 1 p.m. The moment he entered the museum, he observed that the angle between the minute hand and the hour hand of one of the clocks was 20°. While leaving the museum, he observed that the angle between the minute hand and the hour hand of the same clock was 220°. If he spent more than 3 hours and less than 4 hours in the museum, then how much time did he exactly spend in the museum?
(2013)
The radius of the cross-sections of pipes P1 and P2 are 7 m and 14 m respectively. Water flows through P1 at a constant rate of 10 m/s and it can alone fill a tank in 2 hours. If P1 is used as the inlet pipe and P2 as the outlet pipe then together they fill the tank in 4 hours. What is the rate of water flow (in m/s) through P2?
(2012)
A train crosses a platform 100 metres long in 60 seconds at a speed of 45 km per hour. The time taken by the train to cross an electric pole, is
(2011)
In a 400 meter race around a circular stadium having a circumference of 1000 meters, the fastest runner and the slowest runner reach the same point at the end of the 5th minute, for the first time after the start of the race. All the runners have the same starting point and each runner maintains a uniform speed throughout the race. If the fastest runner runs at twice the speed of the slowest runner, what is the time taken by the fastest runner to finish the race?
(2011)
A ship 55 kms. from the shore springs a leak which admits 2 tones of water in 6 min ; 80 tones would suffer to sink her, but the pumps can throw out 12 tones an hour. Find the average rate of sailing that she may just reach the shore as she begins to sink.
(2011)
It takes 6 technicians a total of 10 hours to build a new server from direct computer, with each working at the same rate. If six technicians start to build the server at 11 : 00 am, and one technician per hour is added beginning at 5 :00 pm, at what time will the server be completed?
(2010)
A watch, which gains time uniformly, was 5 minutes behind the correct time when it showed 11:55 AM on Monday. It was 10 minutes ahead of the correct time when it showed 06:10 PM on the next day. When did the watch show the correct time?
(2010)
|
43 docs|31 tests
|


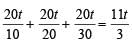 hours
hours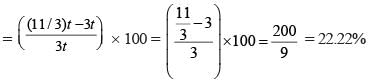
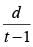
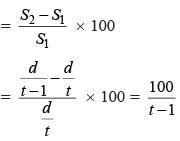


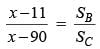 ...(v)
...(v)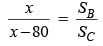
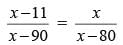

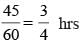

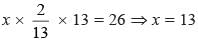
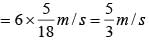
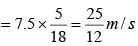
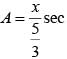
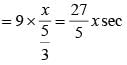
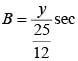
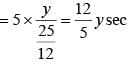
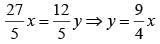 ..(ii)
..(ii)
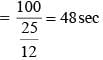
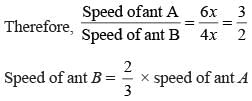

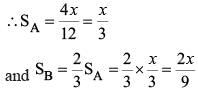
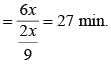
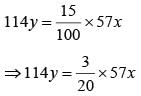

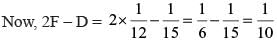
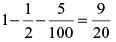

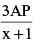
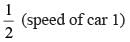
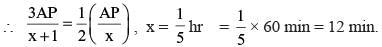
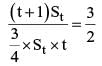
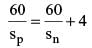 ...(i)
...(i)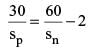 ...(ii)
...(ii)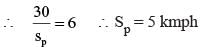
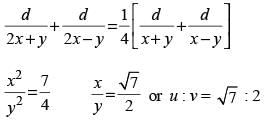
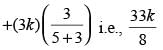
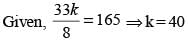
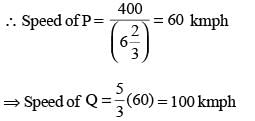
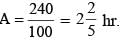
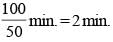
 min.
min.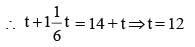
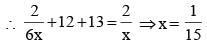
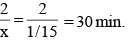

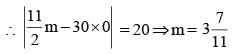
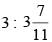 p.m. and 4 p.m.
p.m. and 4 p.m.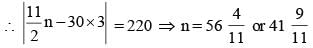
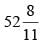 minutes or 3 hours
minutes or 3 hours 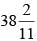 minutes.
minutes.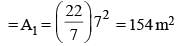
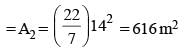

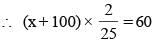
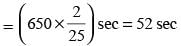

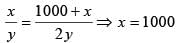

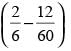 tonnes / min.
tonnes / min.