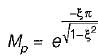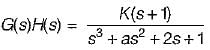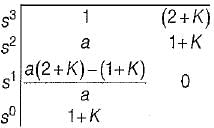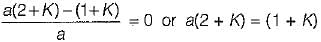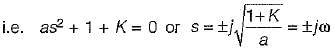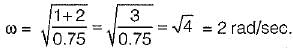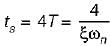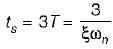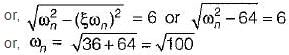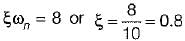Test: Time Domain Analysis of Control Systems- 3 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Time Domain Analysis of Control Systems- 3
For the given series RLC circuit, damping ratio (ξ) and undamped natural frequency (ωn) are respectively given by
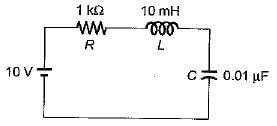

For the unity feedback control system shown below, by what factor the amplifier gain K should be multiplied so that the damping ratio is increased from 0.3 to 0.9?


A system is shown in figure below
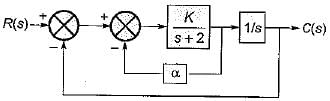
What are the values of K and α respectively so that the system has a damping ratio of 0.7 and an undamped natural frequency ωn of 4 rad/sec ?

What are the values of K and α respectively so that the system has a damping ratio of 0.7 and an undamped natural frequency ωn of 4 rad/sec ?
For type-2 system, the steady state error due to parabolic input is
The open loop transfer function of a unity-feedback control system with unit step input is given by:
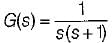
The settling time of the system for 5% tolerance band is,
The integral of a ramp function becomes
Consider a unity feedback control system as shown in figure below:

The error signal e(t) for a unit ramp input for T ≥ 0 is
A second order system has a closed loop transfer function
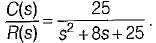
If the system is initially at rest and subjected to a unit step input at t = 0, the third peak in the response will occur at
A closed servo system is represented by the differential equation
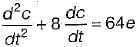
where c is the displacement of the output shaft r is the displacement of the input shaft anc e = r - c.
The damping ratio and natural frequency for this system are respectively
The poles of a closed loop control system art located at -1 ± j.
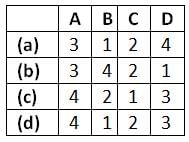
For the given system match List-I (Time domain specifications) with List - II (Values) and select the correct answer using the codes given below the lists
List - I
A. Damping ratio
B. Undamped natural frequency (rad/s)
C. Damping factor
D. Settling time (in secs)
List - II
1. 4.0
2. 1.0
3. 0.707
4. 1.414
Codes:
Consider the block diagram of a control system shown below.
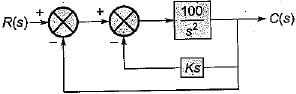
What is the value of gain k such that the system is non oscillatory yet has the lowest possible settling time to step input?
Assertion (A): The "dominant pole" concept is used to control the dynamic performance of the system, whereas the “insignificant poles” are used for the purpose of. ensuring that the controller transfer function can be realized by physical components.
Reason (R): if the magnitude of the real part of a pole is at least 5 to 10 times that of a dominant pole or a pair of complex dominant poles, the pole may be regarded as insignificant in so far as the transient response is concerned.
Assertion (A): The step-function input represents an instantaneous change in the reference input.
Reason (R): If the input is an angular position of a mechanical shaft, a step input represents the sudden rotation of the shaft.
(a) Both A and R are true and R is a correct explanation of A.
(b) Both A and R are true but R is not a correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Consider the following statements related to second order control system with unit step input:
1. The right-half s-plane corresponds to negative damping.
2. Negative damping gives a response that doesn’t grows in magnitude without bound with time.
3. The imaginary axis corresponds to zero damping.
4. The maximum overshoot is often used to measure the relative stability of a control system.
5. Higher the damping in the system larger is the peak overshoot in the transient response of the system.
Which of the above statements is/are correct?
Which of the following is not true regarding addition of a pole to the forward-path transfer function?
For a second-order prototype system, when the undamped natural frequency is increased, the maximum overshoot of the output will
Consider a unity feedback system shown in figure below where, K > 0 and a > 0.
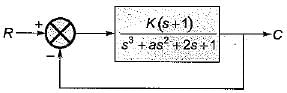
What are the values of k and a respectively so that the system oscillates at a frequency of 2 rad/sec?
The transient response of a system is mainly due to
A second order system has a damping ratio ξ and undamped natural frequency of oscillation ωn respectively. The settling time at 5% of tolerance band of the system is
The unit impulse response of a linear time invariant second order system is
g(t) = 10e-8t sin 6t (t ≥ C)
The natural frequency and the damping ratio of the system are respectively


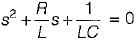
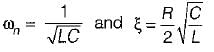

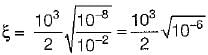
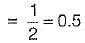
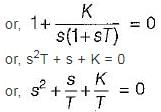
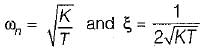
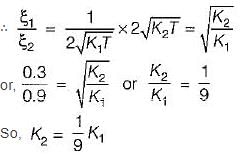

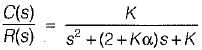
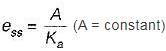
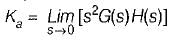
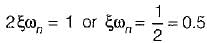
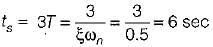
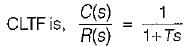
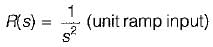
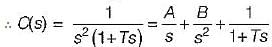
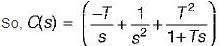
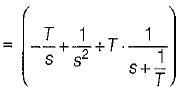
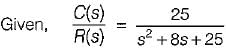
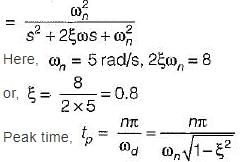
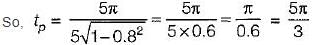
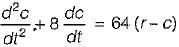
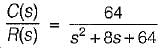
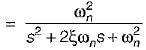
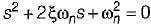
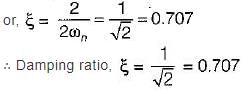
 Damping factor = ξωn = 1
Damping factor = ξωn = 1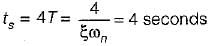
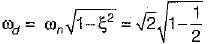
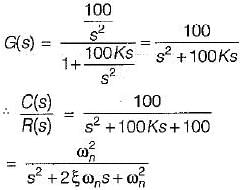
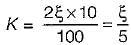

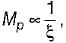 therefore higher is the damping in the system, less is the peak overshoot of the system. Hence, statement-5 is not correct
therefore higher is the damping in the system, less is the peak overshoot of the system. Hence, statement-5 is not correct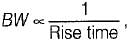 therefore rise time will increase.
therefore rise time will increase.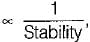 therefore stability will decrease.
therefore stability will decrease.