Test: Translational Motion and Calculations - 1 - MCAT MCQ
10 Questions MCQ Test - Test: Translational Motion and Calculations - 1
A police car accelerates quickly to 60 meters per second in order to pursue a minivan that is recklessly speeding along the highway at 45 meters per second. How long will it take the police car to catch up if the minivan is 600 meters ahead of the police car at the beginning of the chase?
At time t = 1 min the car is traveling at a velocity of 20 meters per second, and at time t = 2 min the car reaches a velocity of 40 meters per second. Which statement best describes the car’s motion during this time interval?
An object is dropped from the top of the Empire State Building. Which of the following statements best describes the motion of the object as it experiences air resistance during its downward fall?
Which of the following statements best represents an example of instantaneous velocity?
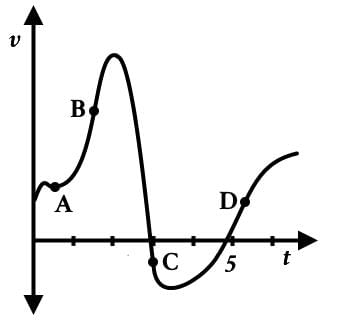
According to the velocity-time graph below, which of the following best characterizes the magnitude of acceleration and displacement at point B as compared with point C?
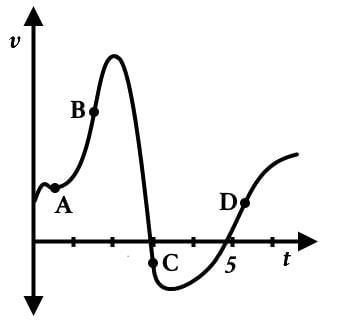
According to the velocity-time graph below, how many times does the particle attain zero acceleration during the entire path?
Which of the following figures below represents an object that is moving at a constant velocity?
Based on the velocity-time graph below, which of the following statements best characterizes the car’s motion?

Based on the displacement-time graph below, which of the following statements accurately describes the car’s motion?
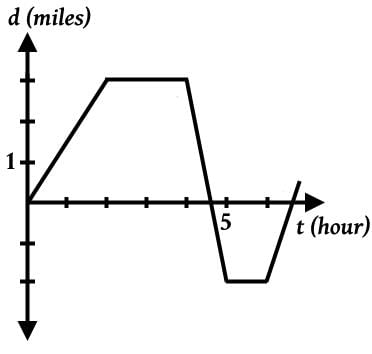
A car travels from point A to B in 3 hours and returns back to point A in 5 hours. Points A and B are 150 miles apart along a straight highway. Which of the following statements most accurately describes the motion of the car?