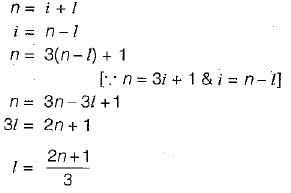Test: Trees- 1
10 Questions MCQ Test Question Bank for GATE Computer Science Engineering | Test: Trees- 1
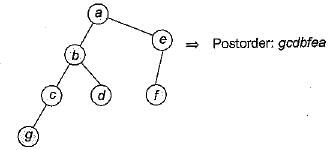
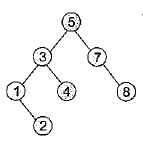
A binary tree T has n leaf nodes. The number of nodes of degree 2 in T is
Because for 2 degree node, every time ‘2’ leafs are added and number of nodes increases is '1'. So number of nodes with degree 2 is always one less than number f leafs present in tree.
Which of the following sequences denotes the post order traversal sequence of the tree of above question?
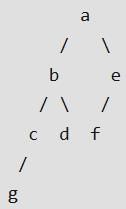
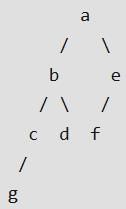
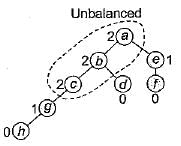
In the balanced binary tree in the figure given below, how many nodes will become unbalanced when a node is inserted as a child of the node "g”?
When a node is added as a child of g.
Nodes a, b and c become unbalanced.
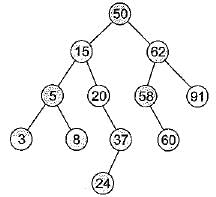
A binary search tree is generated by inserting in order of the following integers: 50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24. The number of nodes in the left subtree and right subtree of the root respectively is
The binary search tree is
The number of nodes in the left subtree and right subtree of the root respectively is (7, 4).
A binary search tree contains the values 1,2,3, 4, 5, 6, 7, 8. The tree is traversed in pre-order and the values are printed out. Which of the following sequences is a valid output?
(a) 53124786
6 can not be child of 8.
(b) 5312648
4 can not be child of 6.
(c) 53241678
1 can not be child of 4 or 5.
Which of the following statements is false?
A labelled rooted binary tree can not be constructed uniquely when inorder traversal is given along with post-order or pre-order traversal.
A complete n-ary tree is one in which every node has 0 or n sons. If x is the number of internal nodes of a complete n-ary tree, the number of leaves in it is given by
In n-ary tree the total number of vertices are m = nx + 1
Where x: number of internal nodes and let l be the number of leaf nodes.
x + l = nx +1
l = (n - 1)x + 1
So number of leaf nodes in n-ary tree with x internal nodes is (n - 1) x + 1.
Consider the following nested representation of binary trees: (X Y Z) indicates Y and Z are the left and right subtrees, respectively, of node X. Note that Y and Z may be NULL, or further nested. Which of the following represents a valid binary tree?
(1 (2 3 4) (5 6 7))
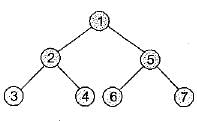
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal. Respectively, of a complete binary tree. Which of the following is always true?
Because of complete binary tree option (b) is always correct.
The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is
In m-ary tree
Total number of nodes = m(internal nodes) + 1
Here, n = 3i + 1
Total nodes = Internal nodes + Leaf nodes
Where l is leaf nodes.
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
Download free EduRev App
Similar Content
 |
|
 |
|
|
|
|
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|