Test: Triangles- 1 - GRE MCQ
20 Questions MCQ Test - Test: Triangles- 1
ABC is a triangle in which AB = 4 cm and BC = 7cm. What is the possible range of values of CA?
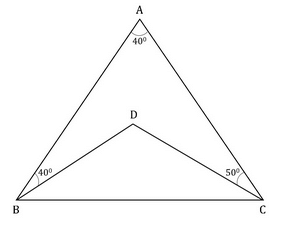
ABC and BDC are two triangles as shown in the given figure. If BDC is an isosceles triangle in which BD = DC. Find the value of ∠BDC.
In the given figure, AB = 6cm. Find the area of the triangle ADC.
- CD = 4cm
- Angle BAD = 30o and Angle ADC = 120o
In the given figure, AE is perpendicular to BC and BD = DC. If the area of triangle ABD = 6cm2, what is the area of triangle ADC?
From the given diagram, find the area of triangle ABC.
- po = qo
- The product of AB and AC is 9.
In the triangle above, Is AB > AC > BC?
I. y1 = c1
II. y1 = 60o
In the figure shown above, point E is the intersection point of the diagnoals AC and BD of rectangle ABCD. Is AB greater than BC?
- AE = 5 cms and AB = 7.25 cm
- The perimeter of AEB is greater than the perimeter of BEC
A right angled triangle, right angled at point B has angles such that a<c<b where a, b, c correspond to the angles at points A, B, C. If the area of the triangle is 2 which of the following inequality indicates the range of values of side BC.
In the given isosceles triangle, if AB = BC = 2 and x = 22.5°, what is the area of the triangle?
In the triangle above, what is the measure of Angle YZX?
(1) Angle YWX = angle WYX = 30°
(2) Triangles WXY and XYZ are isosceles triangles
Is the perimeter of triangle ABC greater than 6 cm?
(1) One side of triangle ABC measures 3 cm
(2) The lengths of the three sides of triangle ABC are consecutive integers
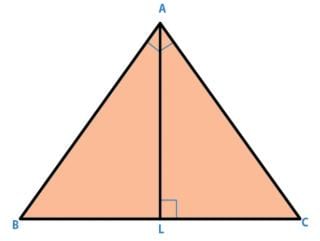
In a triangle ABC,∠ A = 900, AL is drawn perpendicular to BC, Then ∠ BAL is equal to:
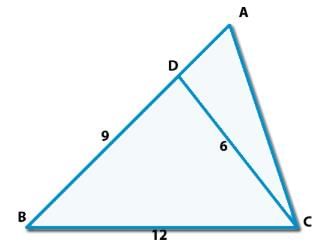
Consider the triangle shown in the figure where BC = 12 cm, Db = 9 cm, CD = 6 cm and What is the ratio of the perimeter of the triangle ADC to that of the triangle BDC ?
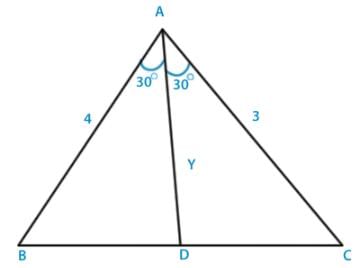
In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and ∠ A = 600, then length of AD is :
The point of intersection of the altitudes of a triangle is called its:
In Δ PQR, PS is the bisector of ∠ P and PT ⊥ OR, then ∠ TPS is equal to:
Two right angled triangles are congruent if :
I.The hypotenuse of one triangle is equal to the hypotenuse of the other.
II.a side for one triangle is equal to the corresponding side of the other.
III.Sides of the triangles are equal.
IV. An angle of the triangle are equal.
Of these statements, the correct ones are combination of: