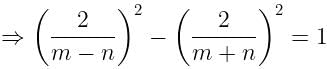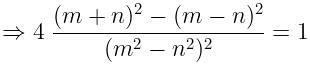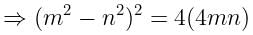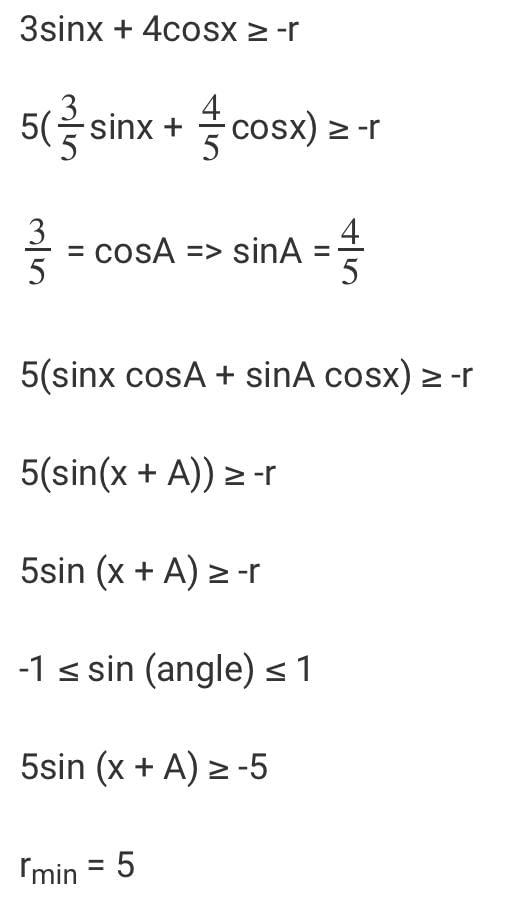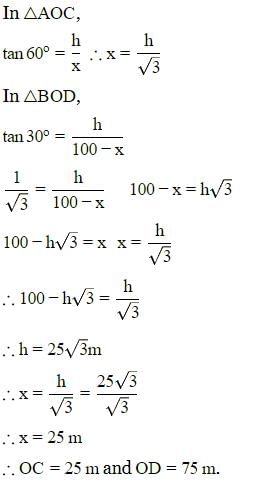Get the App Signup / Login
Sign in Open App

Test: Trigonometry- 1


10 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year | Test: Trigonometry- 1


Description
Attempt Test: Trigonometry- 1 | 10 questions in 20 minutes | Mock test for SSC preparation | Free important questions MCQ to study SSC CGL Tier 2 - Study Material, Online Tests, Previous Year for SSC Exam | Download free PDF with solutions
QUESTION: 1

A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.

Solution:

Let BC be the height of the tower and DC be the height of the student.
In rt. ΔABC,
AB = BC cot 45° = 100 m

In rt. ΔABD, AB = BD cot 60° = (BC + CD) cot 60° = (10 + CD) * (1 / √3)
∵ AB = 100 m
⇒ (10 + CD) * 1 / √3 = 100
⇒ (10 + CD) = 100√3
⇒ CD = 100√3 - 100 = 100 (1.732 - 1) = 100 x 0.732 = 73.2 m

QUESTION: 2

If sin (A + B) = √3 / 2 and tan (A – B) = 1. What are the values of A and B?

Solution:

QUESTION: 3

If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:

Solution:

Cos x – Sin x = √2 Sin x
⇒ Cos x = Sin x + √2 Sin x



⇒ Sin x = (√2 - 1) Cos x
⇒ Sin x = √2 Cos x - Cos x
⇒ Sin x + Cos x = √2 Cos x

QUESTION: 4

If tanØ + sinØ = m, tanØ - sinØ = n, find the value of m2 - n2.
Solution:

Adding the two equations, tanØ = (m + n) / 2
Subtracting the two equations, sinØ = (m - n) / 2

Since, there are no available direct formula for relation between sinØ tanØ.
But we know that: cosec2Ø - cot2Ø = 1




QUESTION: 5

If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of a+b / c+d
Solution:

Cos A = 1 - Cos2A
⇒ Cos A = Sin2A
⇒ Cos2A = Sin4A
⇒ 1 – Sin2A = Sin4A
⇒ 1 = Sin4A + Sin2A
⇒ 13 = (Sin4A + Sin2A)3
⇒ 1 = Sin12A + Sin6A + 3 Sin8A + 3 Sin10A
⇒ Sin12A + Sin6A + 3 Sin8A + 3 Sin10A – 1 = 0

On comparing,
a = 1, b = 3 , c = 3 , d = 1
⇒ (a+b)/(c+d) = 1

Hence, the answer is 1

QUESTION: 6

3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
Solution:

Therefore, the answer is Option A.

QUESTION: 7

A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
Solution:

We know that,
h2 = p2 + b2 Given, p and b are positive integer, so h2 will be sum of two perfect squares.

We see 
a) 72 + 52 = 74
b) 62 + 42 = 52
c) 32 + 22 = 13
d) Can’t be expressed as a sum of two perfect squares

Therefore the answer is Option D.

QUESTION: 8

If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
Solution:

Cos x – Sin x = √2 Sin x 

=> Cos x = Sin x + √2 Sin x 
=> Cos x = Sin x + √2 Sin x 
=> Sin x = Cosx/(√2+1) * Cos x 
=> Sin x = (√2−1)/(√2−1) * 1/(√2+1) * Cos x
=> Sin x = (√2−1)/((√2)2−(1)2)* Cos x
=> Sin x = (√2 - 1) Cos x
=> Sin x = √2 Cos x – Cos x
=> Sin x + Cos x = √2 Cos x

Hence, the correct answer is Option A.

QUESTION: 9

You are standing on the corner of a square whose side length is 25 feet. Standing on the opposite corner from you is a tall tree. The angle of elevation from your position to the top of the tree is exactly 60°. How tall is the tree?
Solution:

First find the distance of the diagonal d along the ground from corner to corner. Using Pythagorean theorem with sides 25 and 25, we get:

252 + 252 = d2

2 × 252 = d2

d = 25√ 2 .

Then to obtain the height h of the tree, use the tangent ratio with angle 60°.

tan 60° = x / (25√ 2 )

√ 3  = x / (25√ 2 )

x = 25√ 2  × √ 3  = 25√ 6 

QUESTION: 10

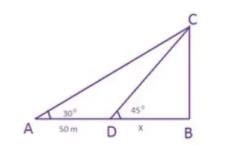
Anil looked up at the top of a lighthouse from his boat and found the angle of elevation to be 30 degrees. After sailing in a straight line 50 m towards the lighthouse, he found that the angle of elevation changed to 45 degrees. Find the height of the lighthouse.
Solution:

If we look at the above image, A is the previous position of the boat. The angle of elevation from this point to the top of the lighthouse is 30 degrees.

After sailing for 50 m, Anil reaches point D from where the angle of elevation is 45 degrees. C is the top of the lighthouse.

Let BD = x

Now, we know tan 30 degrees = 1/ √3 = BC/AB

Tan 45 degrees = 1

=> BC = BD = x

Thus, 1/ √3 = BC/AB = BC / (AD+DB) = x / (50 + x)

Thus x (√3 -1) = 50 or x= 25(√3 +1) m

The answer is Option D.

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us