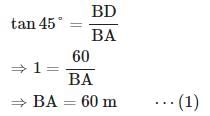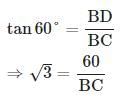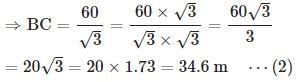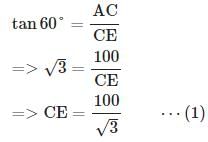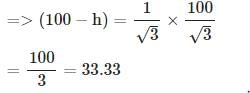Test: Trigonometry- 2 - GMAT MCQ
15 Questions MCQ Test - Test: Trigonometry- 2
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 100 m high, the distance between the two ships is:
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 45º. What is the distance between the base of the tower and the point P?
From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 200 m high, the distance of point P from the foot of the tower is:
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
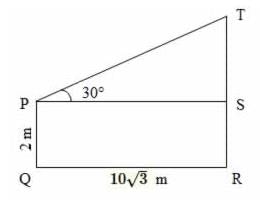
An observer 2 m tall is 10√3 m away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The height of the tower is:
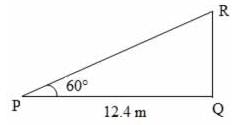
The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 12.4 m away from the wall. The length of the ladder is:
A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to :
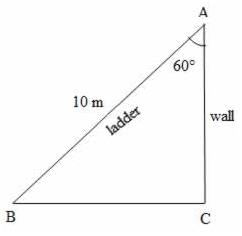
A ladder 10 m long just reaches the top of a wall and makes an angle of 60° with the wall.Find the distance of the foot of the ladder from the wall (√3=1.73)
From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
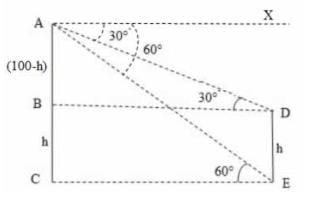
From the top of a hill 100 m high, the angles of depression of the top and bottom of a pole are 30° and 60° respectively. What is the height of the pole?


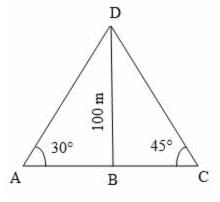
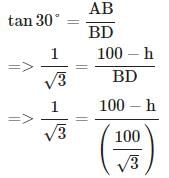
 BAD = 30° ,
BAD = 30° ,  BCD = 45°
BCD = 45°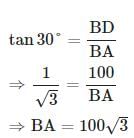
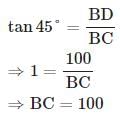

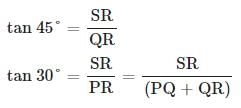

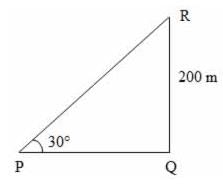
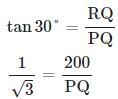
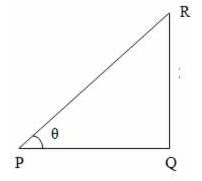
 QPR = θ
QPR = θ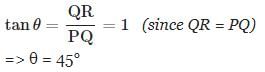



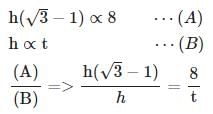
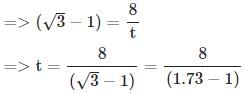
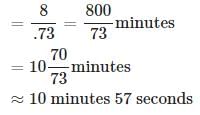
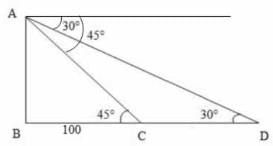
 ACB = 45° ,
ACB = 45° ,  ADC = 30°, BC = 100 m
ADC = 30°, BC = 100 m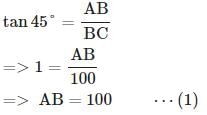
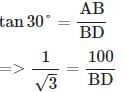
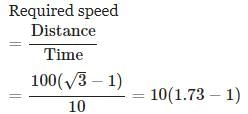
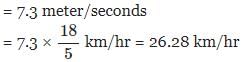
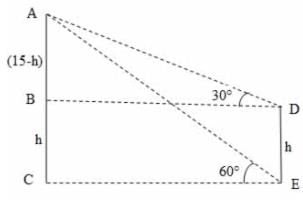
 ADB = 30°,
ADB = 30°,  AEC = 60°
AEC = 60°

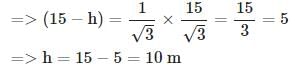
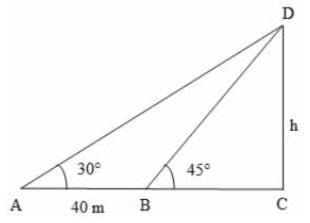
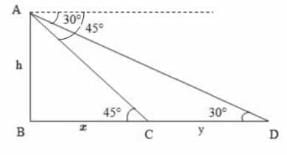
 DAC = 30°,
DAC = 30°,  DBC = 45°
DBC = 45°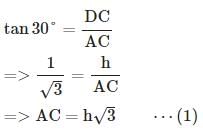
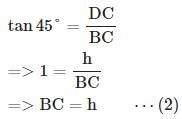

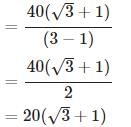
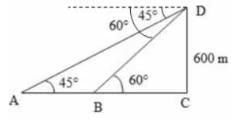
 DAC = 45°,
DAC = 45°,  DBC = 60°
DBC = 60°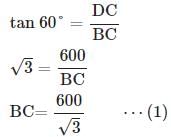
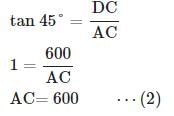
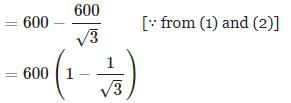
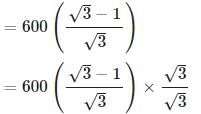
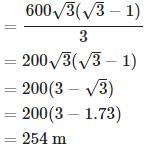
 BAC = 60°
BAC = 60°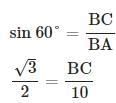
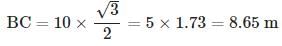

 DAB = 30°
DAB = 30°  ABC =
ABC =  DAB = 30° (because DA || BC)
DAB = 30° (because DA || BC)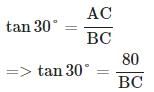
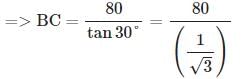
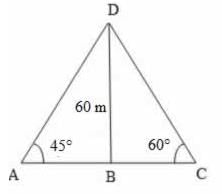
 BAD = 45° ,
BAD = 45° ,  BCD = 60°
BCD = 60°