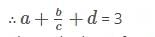Test: Trigonometry- 2 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Trigonometry- 2
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Trigonometry" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. 3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
Sin2014x + Cos2014x = 1, x in the range of [-5π, 5π], how many values can x take?
Consider a regular hexagon ABCDEF. There are towers placed at B and D. The angle of elevation from A to the tower at B is 30 degrees, and to the top of the tower at D is 45 degrees. What is the ratio of the heights of towers at B and D?
Find the maximum and minimum value of 8 cos A + 15 sin A + 15
If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of
In the above figure, the sheet of width W is folded along PQ such that R overlaps S Length of PQ can be written as :-
Find the value of :- (log sin 1° + log sin 2° ………..+ log sin 89°) + (log tan 1° + log tan 2° + ……… + log tan 89°) - (log cos 1° + log cos 2° + ……… + log cos 89°)
Ram and Shyam are 10 km apart. They both see a hot air balloon passing in the sky making an angle of 60° and 30° respectively. What is the height at which the balloon could be flying?
A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower?
Given that cos x + cos y = 1, the range of sin x - sin y is
|
196 videos|217 docs|103 tests
|