Test: Types of Fluid Flow - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Types of Fluid Flow
A beaker contains water up to a certain height as shown. If the water is allowed to get discharged through a small pipe (of a uniform diameter), what type of flow will it be in the pipe?
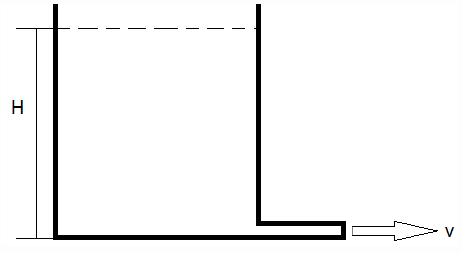
What type of flow can be taken for granted in a pipe of a uniform cross-section?
Which of the following statements is true regarding one and two-dimensional flows?
“The velocity of entrance and exit through a nozzle remains the same.” Is this ever possible?
Three pipe flows named as 1,2 and 3 are observed. The Reynold’s number for the three are 100, 1000 and 10000. Which of the flows will be laminar?
Three flows named as 1,2 and 3 are observed. The flow velocities are v1 and v2. If all other geometrical factors remain the same along with the fluid considered, flow is more likely to be laminar?














