Test: Types of Fluids
10 Questions MCQ Test Fluid Mechanics | Test: Types of Fluids
The relation between shear stress Z and velocity gradient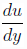 
of a fluid is given by 
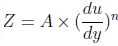where A and n are constants. If n = 1, what type of fluid will it be?
of a fluid is given by where A and n are constants. If n = 1, what type of fluid will it be?Explanation: When n = 1, the relation reduces to Newton’s law of viscosity: z = A * , where A will represent the viscosity of the fluid. The fluid following this relation will be a Newtonian fluid.
The relation between shear stress Z and velocity gradient 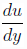of a fluid is given by 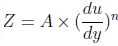where A and n are constants. What type of fluid will it be if n < 1 and n > 1 respectively?
of a fluid is given by where A and n are constants. What type of fluid will it be if n < 1 and n > 1 respectively?Explanation: When n ≠ 1, the relation will be treated as Power law for Non-Newtonian fluids:
. For n < 1, the rate of change of the shear stress decreases with the increase in the value of velocity gradient. Such fluids are called Pseudoplastics.
For n > 1, the rate of change of the shear stress increases with the increase in the value of velocity gradient. Such fluids are called Dilatants.
In the above graph, what types of fluids are represented by the lines 2 and 3 respectively ?
The relation between shear stress Z and velocity gradient of a fluid is given by + B where A, n and B are constants.
Which of the following conditions will hold for a Bingham plastic?
Explanation: For Bingham Plastics, shear stress will not remain constant after an yield value of stress. Thus, A ≠ 0;B ≠ 0. After the yield value, the relation between the shear stress and velocity gradient will become linear. hus, n = 1.
The relation between shear stress Z and velocity gradient of a fluid is given by + B where A, n and B are constants. Which of the following conditions will hold for a Rheopectic?
Explanation: For Rheopectics, shear stress will not remain constant after an yield value of stress. Thus, A ≠ 0; B ≠ 0. After the yield value, the rate of change of the shear stress increases with the increase in the value of velocity gradient. Thus, n > 1.
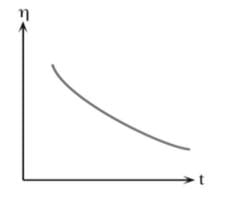
The above graph of viscosity vs time depicts which of the following fluids?
(Hint : This fluid is present in inks and paints)
Explanation: For Thixotropics,their viscosity is time dependent and decreases as time goes on.
The relation between shear stress Z and velocity gradient of a fluid is given by where A and n are constants. The graphs are drawn for three values of n. Which one will be the correct relationship between n1, n2 and n3?
Explanation: The graph corresponding to n = n1 represents Pseudoplastics, for which the rate of change of the shear stress decreases with the increase in the value of velocity gradient. The graph corresponding to n = n2 represents Newtonian fluids, for which shear stress changes linearly with the change in velocity gradient. The graph corresponding to n = n3 represents Dilatents, for which the rate of change of the shear stress increases with the increase in the value of velocity gradient.
Which of the following is a shear-thinnning fluid?
Explanation: Shear-thinning fluids are those which gets strained easily at high values of shear stresses. The relation between shear stress Z and velocity gradient 
of a shear-thinning fluid is given by 
, where A and n are constants and n < 1. This relation is followed by Pseudoplastics.
Which of the following is a shear-thickening fluid?
Explanation: Shear-thickening fluids are those for which it gets harger to strain it at high values of shear stresses. The relation between shear stress Z and velocity gradient 
of a shear-thickening fluid is given by 
where A and n are constants and n > 1. This relation is followed by Dilatants.
What will be the dimension of the flow consistency index for a fluid with a flow behaviour index of -1?
Explanation: The relation between shear stress Z and velocity gradient 
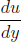of a fluid is given by 
where A is the flow consistency index and n is the flow behaviour index. If n = -1, A = Z * Unit of Z is N/m2 and is s-1. Thus, the unit of A will be N/m2 s.
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
 |
|
 |
|
 |
|
 |
|
|
|
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
Download free EduRev App
Similar Content
 |
|
|
|
 |
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|