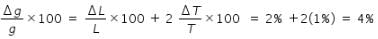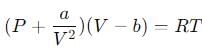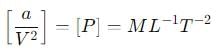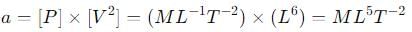Test: Units & Measurement - 3 - JEE MCQ
25 Questions MCQ Test - Test: Units & Measurement - 3
Which of the following sets can enter into the list of fundamental quantities in any system of units ?
If the unit of length is micrometer and the unit of time is microsecond, the unit of velocity will be :
What is the physical quantity whose dimensions are M L2 T-2 ?
If a and b are two physical quantities having different dimensions then which of the following can denote a new physical quantity
Two physical quantities whose dimensions are not same, cannot be :
Which pair of following quantities has dimensions different from each other
If the error in measurement of radius of sphere is 1% , what will be the error in measurement of volume
The velocity 'v' (in cm/s) of a particle is given in terms of time 't' (in s) by the equation
v = at +
The dimensions of a, b and c are
In case of measurement of ‘g’, if error in measurement of length of pendulum is 2%, the percentage error in time period is1 %. The maximum error in measurement of g is
The time dependence of a physical quantity ?
P = P0exp(_at2)
where a is a constant and t is time. The constant a
Force F is given in terms of time t and distance x by
F = A sin C t + B cos D x
Then the dimensions of and
are given by
The Van der Waals equation for 1 mole of a real gas is
where P is the pressure, V is the volume, T is the absolute temperature, R is the molar gas constant and a and b are Van der Waal constants. The dimensions of a are the same as those of
The dimensional formula of coefficient of viscosity is
If force (F) is given by F = Pt_1 + Qt, where t is time. The unit of P is same as that of
The product of energy and time is called action. The dimensional formula for action is same as that for
When a wave traverses a medium, the displacement of a particle located at x at time t is given by y = a sin (bt - cx) where a, b and c are constants of the wave. The dimensions of b/c are the same as those of
The mass of a bag is 1.6 kg. Two objects of mass 20 gm and 15 gm measured to an accuracy of 1 gm are added to it. The total mass of the bag calculated to the correct number of significant figures is



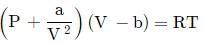
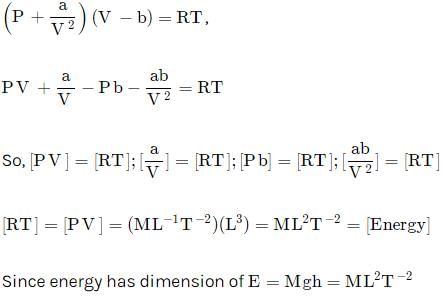

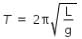
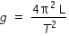 ...........................(1)
...........................(1)