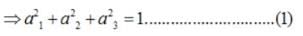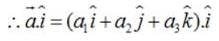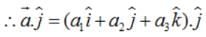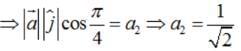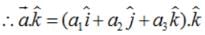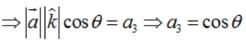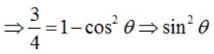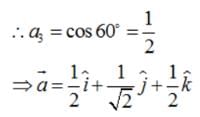Test: Vector Algebra- 1 - JEE MCQ
25 Questions MCQ Test - Test: Vector Algebra- 1
Find the unit vector in the direction of vector where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively
If is a non zero vector of magnitude ‘a’ and λ a non zero scalar, then λ
is a unit vector if
If P1(x1, y1, z1) and P2(x2, y2, z2) are any two points, then the vector joining P1 and P2is the vector P1P2. Magnitude of the vector
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Find a vector in the direction of the vector which has a magnitude of 8 units
are any three vectors then the correct expression for distributivity of scalar product over addition is
Find the direction cosines of the vector joining the points A(1, 2, –3) and B(–1, –2, 1), directed from A to B.
If a unit vector 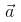 makes angles π/3 with
makes angles π/3 with 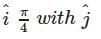 and an acute angle θ with
and an acute angle θ with then find θ
If l, m and n are direction cosines of the position vector OP the coordinates of P are
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
Find the angle between two vectors with magnitudes
and 2, respectively, having
If a unit vector makes angles
and an acute angle θ with
, then the components of
are



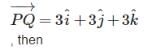
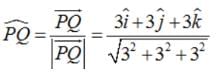
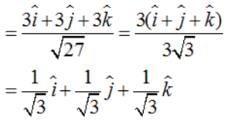

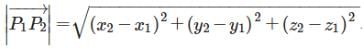

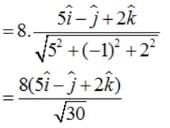
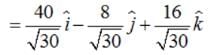
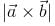 , if
, if 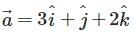 and
and 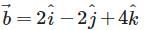
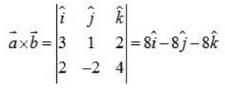
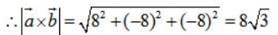


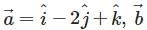
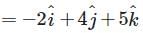 and
and 
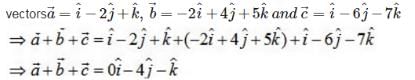
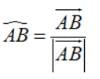
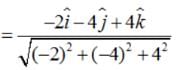
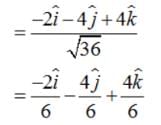
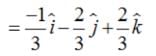
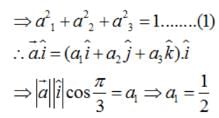

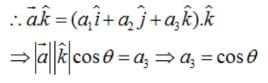


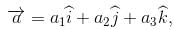 It is given that left|
It is given that left| 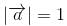 , then ,
, then ,