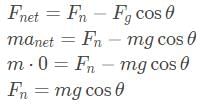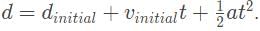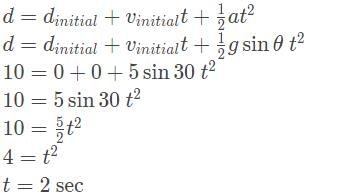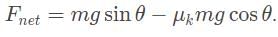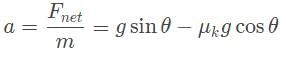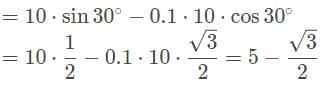All Courses
Get the App Signup / Login
Sign in Open App
MCAT Exam  >  MCAT Tests  >  Physics for MCAT  >  Test: Vector Analysis and Forces Acting on an Object - 3 - MCAT MCQ

Test: Vector Analysis and Forces Acting on an Object - 3 - MCAT MCQ


Test Description

10 Questions MCQ Test Physics for MCAT - Test: Vector Analysis and Forces Acting on an Object - 3

Test: Vector Analysis and Forces Acting on an Object - 3 for MCAT 2025 is part of Physics for MCAT preparation. The Test: Vector Analysis and Forces Acting on an Object - 3 questions and answers have been prepared according to the MCAT exam syllabus.The Test: Vector Analysis and Forces Acting on an Object - 3 MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Vector Analysis and Forces Acting on an Object - 3 below.
Solutions of Test: Vector Analysis and Forces Acting on an Object - 3 questions in English are available as part of our Physics for MCAT for MCAT & Test: Vector Analysis and Forces Acting on an Object - 3 solutions in Hindi for Physics for MCAT course. Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free. Attempt Test: Vector Analysis and Forces Acting on an Object - 3 | 10 questions in 10 minutes | Mock test for MCAT preparation | Free important questions MCQ to study Physics for MCAT for MCAT Exam | Download free PDF with solutions
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 1
Save

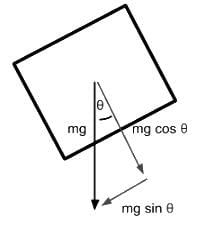
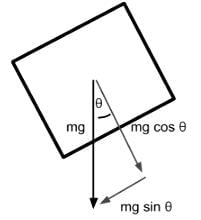
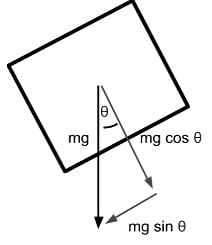
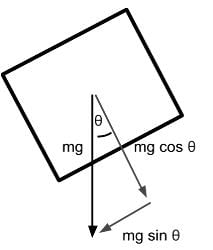
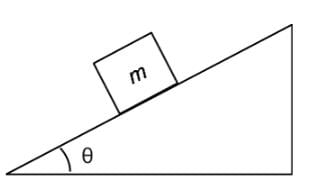
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the normal force on the mass due to the inclined plane?

Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 1
  • Normal force is the contact force that is exerted by a surface onto an object. It acts perpendicular to the surface area and its value will be as large as necessary to prevent sinking through the surface.
  • The only force acting on the box towards the direction of the surface is the gravitational force. However it is not acting directly opposite to the normal force, thus necessitating that the gravitational force split into two perpendicular components.
  • To split our gravitational force into two components, we must orient our coordinate system to the plane’s slope. One axis should run parallel with the plane while another runs perpendicular towards the plane.
  • Since the axis that runs perpendicular to the plane shares the same angle with respect to the gravitational force direction as angle θ, we determine the value of the adjacent component of angle θ to be the gravitational force adjusted by cos θ.
    Gravitational force perpendicular towards the plane surface is cosθ.
  • Since the object is stationary in the direction perpendicular to the plane, we can use Newton’s Second Law on the object to sum our forces together to derive the normal force.

Test: Vector Analysis and Forces Acting on an Object - 3 - Question 2
Save

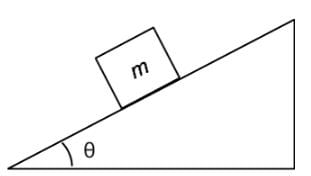
An object of mass m is placed on a frictionless inclined plane as indicated below. Which of the following expressions represent the acceleration of the mass down the inclined plane?

Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 2
  • The only forces on the object include the gravitational force, and the normal force.
  • Since the normal force is acting perpendicular to the acceleration down the incline plane, we do not need to consider its contribution in our determination of the acceleration.
  • The gravitational force is not directly parallel to the plane’s slope, thus necessitating that the gravitational force split into its two perpendicular components.
  • To split our gravitational force into two components, we must orient our coordinate system to the plane’s slope. One axis should run parallel with the plane while another runs perpendicular towards the plane.
  • Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane surface to be mg sinθ. This means that the acceleration is a = F/m , yielding g sin θ
Clear all your doubts with EduRev
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 3
Save

What is the gravitational force experienced by box of mass 50 kg moving down a frictionless plane inclined at a 60°, degrees angle?

Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 3
  • The question stems ask about the gravitational force, not the net force.
  • The gravitational force Fg is caused by the earth’s gravity and acts on the object. Near the surface of the earth, this is defined as the force of gravity g multiplied by the mass of the object.
  • Fg = mg
    Fg = 50⋅9.8 = 490
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 4
Save

A block of mass m is sitting motionless on a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following will occur once the plane is elevated on one side, increasing θ?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 4
  • The coefficients of friction, both kinetic and static, are not affected by the slope angle of the surface and stays constant throughout the elevation. The coefficient of friction is determined experimentally and is usually only affected by the types of materials used in the interface between the surfaces of the object and plane.
  • The maximum force of static friction is proportional to the normal force.
  • The normal force is decreased as the plane is elevated because the component of gravitational force directed into the plane (Fg cosθ) decreases as θ increases. Therefore, as θ increases, the maximum force caused by static friction will decrease.
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 5
Save

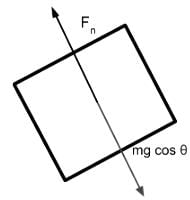
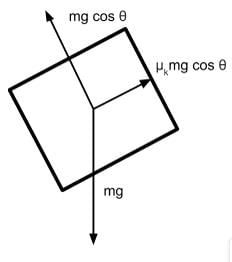
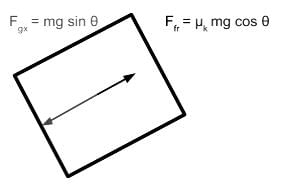
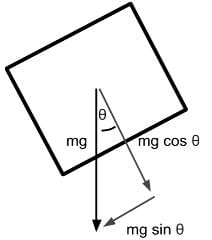
A block of mass m is sliding down on a plane with an incline of θ and a coefficient of kinetic friction of μk as shown below. Which of the following free-body diagrams demonstrates the various forces acting on this block?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 5
  • The normal force is the contact force that is exerted by a surface onto an object. It acts perpendicular to the surface area and its value will be as large as necessary to prevent sinking through the surface. In this case, the normal force must be equal to the component of gravitational force directed into the plane because the block does not move in the direction perpendicular to the plane.
  • The force caused by kinetic friction will be in a direction that opposes motion. Since the block will naturally fall towards the lower side of the ramp, we can determine the force of kinetic friction to be in the direction opposite of the fall.
  • Since the axis that runs perpendicular to the plane shares the same angle with respect to the gravitational force direction as angle θ, we determine the value of the adjacent component of angle θ to be the gravitational force adjusted by cos θ.
    Gravitational force perpendicular towards the plane surface is mg cos θ. Because the block does not sink into the slope, the normal force is also mg cos θ
  • The force caused by kinetic friction will equal the normal force adjusted by the coefficient of friction μk. Thus the correct free-body diagram will have the force of kinetic friction labeled with μk cos θ:
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 6
Save

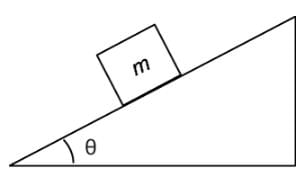
A block of mass m is sliding at a positive constant acceleration down a plane with an incline of θ, a coefficient of static friction of μs, and a coefficient of kinetic friction μk. Which of the following expressions represents the net force on the block? 
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 6
  • The net force expression should be positive with respect to the direction of motion. The block does not move in the direction perpendicular to the plane, therefore we only need to look at the forces affecting the block in the direction parallel to the plane.
  • The forces on the block in the direction parallel to the plane are: the force due to friction (Ffr) and the component of gravitational force parallel to the plane (Fgr).
  • The direction of motion is down the plane, therefore the expression should have the gravitational force parallel to the plane, which is pulling the block down, be subtracted by the force due to friction, which is working in the opposite direction.
  • Since the block is in motion, the coefficient of kinetic friction μk is used. The frictional force is the product of the normal force and the coefficient of kinetic friction μk.
  • Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ and the value of the gravitational force perpendicular to the plane (also the value of the normal force) to be mg cos θ. Therefore, the frictional force is uk mg cos θ.

    Free-body diagram of the block of mass m
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 7
Save

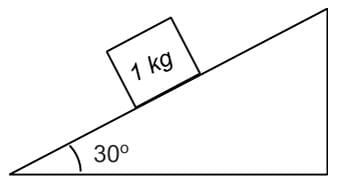
An object of mass m = 1 kg is initially placed on a frictionless plane, inclined by an angle θ = 30° as indicated below. How long does it take the mass to move the distance of 10 m down the incline?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 7
  • Since we are given the distance and we need to determine the time, we are going to have to first derive the acceleration. The kinematics equation of interest that includes all of these variables is 
  • Since the object is initially placed on a frictionless plane, the initial velocity is 0. We are defining the final distance as the point where the block moves 10 m, so the initial distance is 0.
  • Since the slope is frictionless, the only force acting on the object in the axis parallel to the slope is the component of gravitational force parallel to the slope, mg sin θ.
  • The net acceleration is derived from the net force, mg sin θ, divided by the mass. This yields g sin θ.
  • Now that we have derived all the terms of our relevant kinematics equation, we can solve for the time:

    *assuming g = 10 is a good shortcut for physics problems
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 8
Save

An 8 kg block is placed at the top of a plane inclined by 30° with a coefficient of kinetic friction of 0.1. What is the block’s acceleration down the ramp?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 8
  • To obtain the acceleration, we must obtain the net force. A free-body diagram will show the forces acting on the block is motionless in the direction perpendicular to the plane but is present in the direction parallel into the plane.
  • The two forces acting on the block are mg sin θ, the component of gravitational force acting downwards along the plane, and Ff the force of kinetic friction acting directly against motion and upwards along the plane.
  • Frictional force is the product of the normal force and the coefficient of kinetic friction: Ff = μkFN 
  • Since the axis that runs perpendicular to the plane shares the angle θ with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ and the value of the gravitational force perpendicular to the plane (also the value of the normal force) to be mg cos θ. Therefore, the frictional force is Ff = μk mg cos θ.
  • The net force down the ramp is the difference between the two forces:

    Dividing Fnet by m gives us net acceleration:

    Replacing the variables with numbers we get:
     
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 9
Save

Which of the following changes would increase the net acceleration of mass m down the frictionless inclined plane?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 9
  • The net acceleration of mass m down the frictionless inclined plane is determined by the net force acting on mass m.
  • The only force acting on mass m in the direction of the incline is the component of gravitational force represented by the equation mg sin θ. Therefore, the net acceleration of mass m is represented by the equation g sin θ.
  • Where the mass is released along the inclined plane does not affect the forces acting on the mass. Therefore the net acceleration of mass m down the inclined plane is not affected by the distance the mass travels along the plane.
  • While the net force is proportional to the mass, the net acceleration is not: a = g sin θ. Increasing the angle of θ will increase the net acceleration as a larger component of gravitational force will act on the mass in the downward direction.
Test: Vector Analysis and Forces Acting on an Object - 3 - Question 10
Save

What happens to the acceleration of a block as it moves down a frictionless inclined plane?
Detailed Solution for Test: Vector Analysis and Forces Acting on an Object - 3 - Question 10
  • To obtain the acceleration, we must obtain the net force. A free-body diagram will show the forces acting on the block is motionless in the direction perpendicular to the plane but is present in the direction parallel into the plane.
  • Since the axis that runs perpendicular to the plane shares the same angle with respect to the direction of gravitational force, we determine the value of the gravitational force down the slope of the plane’s surface to be mg sin θ. Since no other forces oppose it in this direction, this is also the net force,
  • Dividing Fnet by m gives us net acceleration: a = g sin θ.
  • Assuming θ and g is constant, acceleration is constant while the block moves down the frictionless inclined plane.
158 videos|9 docs|21 tests
Join Course
Information about Test: Vector Analysis and Forces Acting on an Object - 3 Page
In this test you can find the Exam questions for Test: Vector Analysis and Forces Acting on an Object - 3 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Vector Analysis and Forces Acting on an Object - 3, EduRev gives you an ample number of Online tests for practice
158 videos|9 docs|21 tests
Join Course
Download as PDF

Important Questions for Vector Analysis and Forces Acting on an Object - 3

Find all the important questions for Vector Analysis and Forces Acting on an Object - 3 at EduRev.Get fully prepared for Vector Analysis and Forces Acting on an Object - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Vector Analysis and Forces Acting on an Object - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Vector Analysis and Forces Acting on an Object - 3 resources.

Vector Analysis and Forces Acting on an Object - 3 MCQs with Answers

Prepare for the Vector Analysis and Forces Acting on an Object - 3 within the MCAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Vector Analysis and Forces Acting on an Object - 3 Physics for MCAT

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Vector Analysis and Forces Acting on an Object - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup