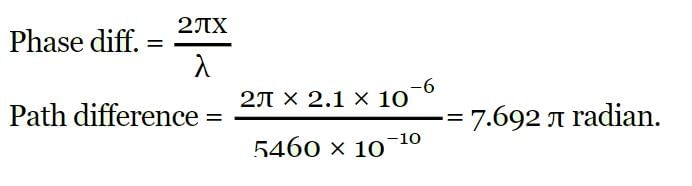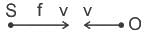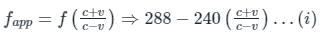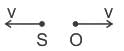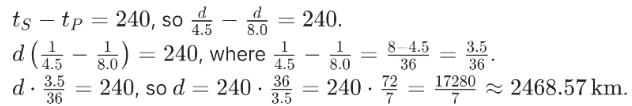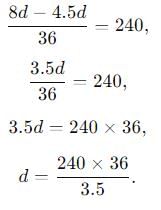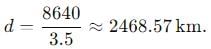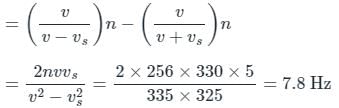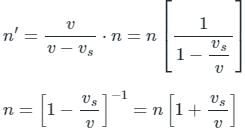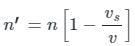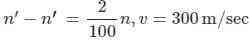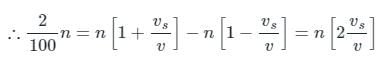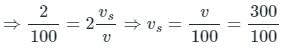Test: Waves-1 - JEE MCQ
20 Questions MCQ Test - Test: Waves-1
The path difference between two wavefronts emitted by coherent sources of wavelength 5460 Å is 2.1 micron . The phase difference between the wavefronts at that point is _
The path difference between two waves
y1= A1 sin wt and y2= A2 cos (wt + f) will be
y1= A1 sin wt and y2= A2 cos (wt + f) will be
The resultant amplitude in interference with two coherent source depends upon _
A source (S) of sound has frequency 240 Hz. When the observer (O) and the source move towards each other at a speed v with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be 288 Hz. However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be n Hz. The value of n is _______.

An earthquake generates both transverse (S) and longitudinal (P) sound waves in the earth. The speed of S waves is about 4.5 km/s and that of P waves is about 8.0 km/s. A seismograph records P and S waves from an earthquake. The first P wave arrives 4.0 min before the first S wave. The epicenter of the earthquake is located at a distance about:
An earthquake generates both transverse (S) and longitudinal (P) sound waves in the earth. The speed of S waves is about 4.5 km/s and that of P waves is about 8.0 km/s. A seismograph records P and S waves from an earthquake. The first P wave arrives 4.0 min before the first S wave. The epicenter of the earthquake is located at a distance about:
A source of the sound of frequency 256 Hz is moving rapidly towards a wall with a velocity of 5 m/s. The speed of sound is 330 m/s. If the observer is between the wall and the source, then beats per second heard will be.
The difference between the apparent frequency of a source of sound as perceived by an observer during its approach and recession is 2% of the natural frequency of the source. If the velocity of sound in air is 300 m/sec, the velocity of the source is (It is given that velocity of source << velocity of sound)
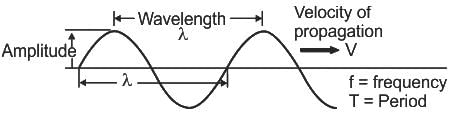
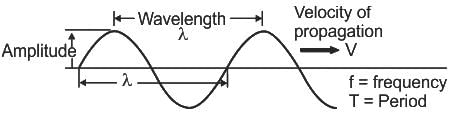
How long will a sound wave take to travel 1.5km, which has a frequency of 5 kHz and wavelength of 6 cm?
The waves with the frequency above the audible range of human beings are called _______.
The frequency of a sound wave is 200 Hz and its wavelength is 2 m. What is the speed of the sound wave?
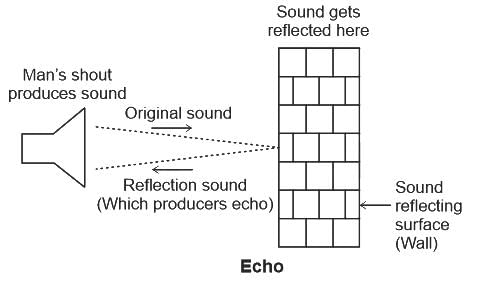
A man standing on a cliff hears the echo of his shout after 1 s. If the velocity of sound in air is 340 m/s, what is the distance between the man and the mountain from which his voice is reflected?
Calculate the speed of a sound wave whose wavelength is 0.5 m and frequency is 640 Hz.