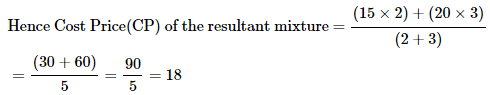Test: Word Problems - 1 - GMAT MCQ
20 Questions MCQ Test GMAT Mock Test Series 2025 - Test: Word Problems - 1
The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
Four numbers in the ratio of 1:3:4:7 add up to give a sum of 75. Find the value of the biggest number.
During a trip, Charles covered the first part of a certain distance at an average speed of 30 miles per hour and the remaining part at an average speed of 50 miles per hour. If the ratio of time taken to cover the first part and remaining part is 2: 3, then what is the total distance that Charles travelled?
(1) It took a total of 5 hours to complete the entire distance.
(2) 2/7th of the entire distance was covered during the first part
Two dogs are running towards each other from opposite ends of a two-mile track. Dog 1 has a speed of 12 mph and Dog 2 has a speed of 8 mph. How many miles from Dog 1’s starting position will they meet?
Riding her bicycle downhill, Sam reached the bottom of the 10-mile trail 10 minutes faster than it took her, riding 12 miles per hour, to reach the top of the trail. What was her downhill speed?
A positive number Y is first increased by 10% then decreased by 50% and then increased by 100%. The series of successive changes to Y is equivalent to a single change of
Operating at their respective constant rates, Photocopying machine B takes 6 minutes more than photocopying machine A to copy x pages. When machines A and B are operated simultaneously, 7x pages can be copied in 20 minutes. In how many minutes can machine A operating alone copy 2x pages?
Peter, Mark and John work in the marketing department of an e-learning firm. Peter can answer 25 emails in an hour, Mark can answer 40 percent more emails in an hour than Peter and John takes 1/6 lesser time to answer the same number of emails as Peter. By what percentage should Peter increase his speed so that the three employees can together answer 1/6 more emails than they currently do?
A triangle is to be constructed in the xy-plane such that the x- and y- coordinates of each vertex are integers that satisfy the inequalities -3 ≤ x < 7 and 2 < y ≤ 7. If one of the sides is parallel to the x-axis, how many different triangles with these specifications can be constructed?
What is the probability that a person born between the years 1990 and 2010, inclusive, was born in a leap year?
From a set of consecutive numbers from 1 to 20 (both inclusive) a number is selected. What is the probability that the selected number is divisible by 5?
In what time will Rs. 72 become Rs. 81 at 25/4% per annum simple interest?
The cost of Type 1 material is Rs. 15 per kg and Type 2 material is Rs.20 per kg. If both Type 1 and Type 2 are mixed in the ratio of 2 : 3, then what is the price per kg of the mixed variety of material?
Out of the 150 students of School X, 40 students have opted for only French as an extra subject. Some students have opted for German as an extra subject and 30 students have opted neither for German nor French. What is the total number of students who have opted for only German?
(1) The total number of students opting for at least one subject out of German and French is 120.
(2) The number of students who opted for both German and French is one-third of the number of students who opted for neither of the two subjects.
Out of the 500 GMAT aspirants who registered on the e-GMAT website a single day, 50% registered for Verbal courses and 200 registered for Quant courses. How many students registered for neither of the Verbal and Quant course?
(1) 30% of the aspirants registered only for Quant courses
(2) 10% of the aspirants registered for both Quant and Verbal courses
A machine costs Rs. 1025. If it is sold at a loss of 25%, what will be its cost price as a percentage of its selling price?
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
A Tank is filled with the mixture of Milk and Water in the ratio of 3:2 up to 2/5 of its capacity. The tank has two inlet pipes i.e., Milk and Water inlets. Milk and Water pipe can fill an empty tank in 12 and 18 hours respectively. Now both pipes are opened simultaneously and closed after the Tank is completely filled, then what is the ratio of Milk and Water in the full Tank if it can accommodate 250Litre?
|
18 docs|33 tests
|