Test: Word Problems - JEE MCQ
10 Questions MCQ Test - Test: Word Problems
In drilling world’s deepest hole, it was found that the temperature T in degree Celsius, x km below the surface of Earth, was given by T = 30 + 25 (x – 3), 3 < x < 15. If the required temperature lies between 200o C and 300o C, then the depth, x will lie between
A solution of 10% boric acid is to be diluted by adding a 4% boric acid solution to it. The resulting mixture is to be more than 5% but less than 8% boric acid. If we have 750 litres of the 10% solution, then the quantity of the 4% solution that has to be added will lie between
Pairs of consecutive even positive integers, both of which are larger than 7 such that their sum is less than 28, are
The longest side of a triangle is 4 times the shortest side and the third side is 4 cm shorter than the longest side. If the perimeter of the triangle is at least 59 cm, then the minimum length of the shortest side is
In an experiment a solution of hydrochloric acid is to be kept between 30 and 35 degree celcius. What is the range of temperature in degree Fahrenheit if conversion formula is given by 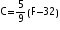 ,where C and F represent temperature in degree celsius and degree fahrenheit, respectively?
,where C and F represent temperature in degree celsius and degree fahrenheit, respectively?
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 6 cm longer than the shortest and the third length is to be thrice as long as the shortest. If the third piece is to be at least 4 cm longer than the second, then the length of the shortest board will lie between
A plumber can be paid under two schemes as given below:
I: Rs 600 and Rs 50 per hour.
II: Rs 170 per hour.
If the job takes n hours, then the values of n for which the scheme I will give the plumber better wages are
In the first four examinations, each of 100 marks, Dipika got 94, 73, 72, 84 marks. If a final average greater than or equal to 80 and less than 90 is needed to obtain a final grade B in a course, then the range of marks, Dipika must score in the fifth examination in order to obtain grade B is
The cost and revenue functions of a product are given by C(x) = 2x + 400 and R(x) = 6x + 20 respectively, where x is the number of items produced by the manufacturer. The minimum number of items that the manufacturer must sell to realize some profit is
IQ of a person is given by the formula 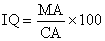 , where M A is mental age and CA is chronological age. If 85 < IQ < 145 for a group of 12-year children, then the mental age will lie between
, where M A is mental age and CA is chronological age. If 85 < IQ < 145 for a group of 12-year children, then the mental age will lie between















