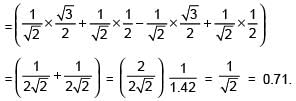All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Test: XAT Quant 2017 - CAT MCQ

Test: XAT Quant 2017 - CAT MCQ


Test Description

27 Questions MCQ Test - Test: XAT Quant 2017

Test: XAT Quant 2017 for CAT 2024 is part of CAT preparation. The Test: XAT Quant 2017 questions and answers have been prepared according to the CAT exam syllabus.The Test: XAT Quant 2017 MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: XAT Quant 2017 below.
Solutions of Test: XAT Quant 2017 questions in English are available as part of our course for CAT & Test: XAT Quant 2017 solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: XAT Quant 2017 | 27 questions in 40 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test: XAT Quant 2017 - Question 1
Save

The sum of series, (–100) + (–95) + (–90) + .............. + 110 + 115 + 120, is:

Detailed Solution for Test: XAT Quant 2017 - Question 1
The series can be written as follows: 105 + 110 + 115 + 120 = 450. Thus, Option D is the correct answer.

Test: XAT Quant 2017 - Question 2
Save

Four two-way pipes A, B, C and D can either fill an empty tank or drain the full tank in 4, 10, 12 and 20 minutes respectively. All four pipes were opened simultaneously when the tank is empty.

Q. Under which of the following conditions the tank would be half filled after 30 minutes?

Detailed Solution for Test: XAT Quant 2017 - Question 2
Tank get half-filled in 30 minutes, i.e., in 1 minute 1/60 fraction get filled. Let ‘s check this through options with 1-minute cases

Option (a): 1 / 4 – (1 / 10 + 1 / 12 + 1 / 20) = 1 / 4 – 14 / 60 = 1 / 60(correctanswer)

Option (b): –1/60 (drained)

Option (c): (1 / 10 + 1 / 12) – (1 / 4 + 1 / 20) = 11 / 60 – 18 / 60(drained)

Option (d): 7/60 filled in 1 minute.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: XAT Quant 2017 - Question 3
Save

A shop, which sold same marked price shirts, announced an offer - if one buys three shirts then the fourth shirt is sold at a discounted price of ₹100 only. Patel took the offer. He left the shop with 20 shirts after paying ₹20,000.

Q. What is the marked price of a shirt?

Detailed Solution for Test: XAT Quant 2017 - Question 3

Assume marked price of shirts = x/per shirt

Four shirts will cost (with the offer) = 3x + 100

Then, 20 shirts will cost (5 such offers) = 5(3x + 100) = 15x + 500 = 20000

Thus, x = 19500/15 = 1300.

Therefore, B is the right answer.

 

 

Test: XAT Quant 2017 - Question 4
Save

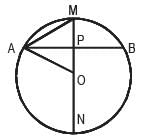
AB is a chord of a circle. The length of AB is 24 cm. P is the midpoint of AB. Perpendiculars from P on either side of the chord meets the circle at M and N respectively. If, PM < PN and PM = 8 cm. then

Q. what will be the length of PN?
Detailed Solution for Test: XAT Quant 2017 - Question 4

AB is a chord and MN is the perpendicular bisector of the chord AB at point P (as PM and PN both are perpendicular to AB). Then, MN is also diameter of the circle. Hence, OA = OM = ON, are the radii of the circle. We need to find PN, which is equal to OP + ON Given, AP = 12 and PM = 8, therefore; OP = (r – 8), where r is radius of the circle. OPA is a right-angle triangle. Hence, 122 + (r – 8)2 = r2

144 + r2 + 64 – 16r = r2

16r = 208, r = 13

If radius is 13, then OP = (13 – 8) = 5

Hence, PN = 5 + 13 = 18.

Test: XAT Quant 2017 - Question 5
Save

If x and y are real numbers, the least possible value of the expression 4(x – 2)2 + 4(y – 3)2 – 2(x – 3)2 is:
Detailed Solution for Test: XAT Quant 2017 - Question 5
4(x – 2)2 + 4(y – 3)2 – 2(x – 3)2

= 4(x2 – 4x + 4) + 4(y2 – 6y + 9) – 2(x2 – 6x + 9)

= 2x2 – 4x + 4y2 – 24y + 34

= 2(x2 – 2x + 1) + 4(y2 – 2.y.3 + 9) + (34 – 2 – 36)

= 2(x – 1)2 + 4(y – 3)2 – 4

= – 4 (assuming minimum value of square terms is zero).

Thus, Option B is the right answer.

Test: XAT Quant 2017 - Question 6
Save

If f(x) = ax + b, a and b are positive real numbers and if f(x)) = 9x + 8, then the value of a + b is:
Detailed Solution for Test: XAT Quant 2017 - Question 6
If f(x) = ax + b, then f(f(x)) = a (ax + b) + b = a2x + ab + b

9x + 8 = a2x + ab + b

Thus, a2 = 9, a = 3.

Moreover, ab + b = 8, or, 3b + b = 8, or, b = 2

So, a + b = 5.

Test: XAT Quant 2017 - Question 7
Save

Arup and Swarup leave point A at 8 AM to point B. To reach B, they have to walk the first 2 km, then travel 4 km by boat and complete the final 20 km by car. Arup and Swarup walk at a constant speed of 4 km/hr and 5 km/hr respectively. Each rows his boat for 30 minutes. Arup drives his car at a constant speed of 50 km/hr while Swarup drives at 40 km/hr. If no time is wasted in transit, when will they meet again?
Detailed Solution for Test: XAT Quant 2017 - Question 7
During the 2 km walk, Arup takes 30 minutes and Swarup takes 24 minutes. Hence, Swarup is ahead of Arup by 6 minutes. In boat, both of them row for 30 minutes. Hence, Swarup maintains the margin of 6 minutes. In car, every hour Arup goes ahead by 10 km. Before Arup starts, in 6 minutes, Swarup covers 4 km. Arup covers this distance in (60/10)*4 = 24 minutes During walk and in boat Arup goes = 30 + 30 = 60 minutes They will meet again at 8 AM + 60 minutes + 24 minutes = 9:24 AM.

Test: XAT Quant 2017 - Question 8
Save

Hari's family consisted of his younger brother (Chari), younger sister (Gouri), and their father and mother. When Chari was born, the sum of the ages of Hari, his father and mother was 70 years. The sum of the ages of four family members, at the time of Gouri's birth, was twice the sum of ages of Hari's father and mother at the time of Hari's birth. If Chari is 4 years older than Gouri, then find the difference in age between Hari and Chari.
Detailed Solution for Test: XAT Quant 2017 - Question 8
Assuming the age of: Hari’s father = F, Hari’s mother = M, Hari = H, when Chari was born. Hence, their ages would be: F – H, M – H and 0, when Hari was born. Similarly, the ages of four other members, at the time of Gouri’s birth, would be: F + 4, M + 4, H + 4, 4. (since Chari is 4 years older than Gouri)

We need to find H. It is given that:

F + M + H = 70 → … (i)

It is also given that:

F + M + H + 16 = 2(F – H + M – H) … (ii)

If we can replace F + M + H from Eq. (1) in Eq. (2) then:

Eq. 2 → 70 + 16 = 2(F + M + H – 3H) (expressing –2H as H – 3H in RHS)

86 = 2(70 – 3H), 6H = 54 H = 9.

Hence, E is the correct answer.

Test: XAT Quant 2017 - Question 9
Save

In a True/False quiz, 4 marks are awarded for each correct answer and 1 mark is deducted for each wrong answer. Amit, Benn and Chitra answered the same 10 questions, and their answers are given below in the same sequential order.

Q. If Amit and Benn both score 35 marks each then Chitra's score will be:
Detailed Solution for Test: XAT Quant 2017 - Question 9
Amit and Benn both got 35 marks. Maximum possible = 40 (if all correct). So they made 1 mistake. (9 correct and one wrong = 9*4 –1= 35). Their answers are all same, except 3rd and 5th number. As they made only 1 mistake, both of them are correct in one of these two. Except 3rd and 5th answers, out of remaining 8, Chitra had 5 mismatches with both of them i.e. 5 mistakes. In 3rd and 5th numbers, her answer was same as Benn. So, one out of 3rd and 5th question is right and the other one is wrong. Hence, she made a total of 6 mistakes and her marks should be = 4 × 4 – 6 = 10.

Test: XAT Quant 2017 - Question 10
Save

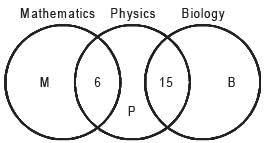
In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50.

Q. What is the maximum possible number of students who major ONLY in Physics?
Detailed Solution for Test: XAT Quant 2017 - Question 10

Total = 60, Math = M + 6, Physics = P + 21, Bio = B + 15

In English,

Total marks by M and B as common English = 50* (Math + Bio)

Total marks by students in Math = 45*(Math)

Total marks by students in Bio = 60*(Bio)

50*(Math + Bio) = 45*(Math) + 60*(Bio)

Or, Math = 2*Bio

Minimum Bio = 15, Minimum Math = 2*15 = 30,

So, the possible maximum students in ONLY Physics should be 60 – 15 – 30 = 15.

Test: XAT Quant 2017 - Question 11
Save

If 5°≤x°≤ 15°, then the value of sin 30° + cos x° – sin x° will be:
Detailed Solution for Test: XAT Quant 2017 - Question 11
Value of Sin (30°) = 1/2, Hence, we need to find the maximum value of (cos x° – sin x°) to solve the question. As value of cosx° decreases as angle moves from 0 to 90 and value of sinx° increases, highest possible value of cosx° – sinx° will be at 50 as it is closer to zero.

The minimum value will be at 150, in the given range of: 5° ≤ x° ≤ 15°. Cos 15° – Sin 15° can be written as: Cos(45° – 300) – Sin(45° – 30°) Applying the formula for Cos (A – B) and Sin(A – B), (Cos 45° × Cos 30° + Sin 45° Sin 30°) – (Sin 45° Cos 30° – Cos45° Sin30°)

This means that 0.71 is the minimum value of the expression (cos x° – sin x°) in the range of x given. Hence, at 150, the value of (sin 300 + cos x° – sin x°) would be (0.5 + .71), which is greater than 1. So, Option E is the right answer.

Test: XAT Quant 2017 - Question 12
Save

The volume of a pyramid with a square base is 200 cm3. The height of the pyramid is 13 cm. What will be the length of the slant edges (i.e., the distance between the apex and any other vertex), rounded to the nearest integer?
Detailed Solution for Test: XAT Quant 2017 - Question 12
Volume = 1/3 × Area of the base (A2) × Height of the pyramid

(H = 13 cm) Thus, 200 = 1/3 × A2 × 13 ⇒ A2 = 600/13

Therefore, side of the square base = A =(√600 / 13)

Say, diagonal of the base = 2B

Then, B2 + B2 = A2 = 600/13

⇒ B2 = 300/13

(Slant edge of pyramid)2 = H2 + B2

Thus, length of the slant edge

Test: XAT Quant 2017 - Question 13
Save

A dice is rolled twice. What is the probability that the number in the second roll will be higher than that in the first?
Detailed Solution for Test: XAT Quant 2017 - Question 13
Out of a total of 36 cases following cases will satisfy the above condition

Dice 1 (1): Dice 2 (2,3,4,5, & 6) i.e., 5 cases

Dice 1 (2): Dice 2 (3,4,5, & 6) i.e., 4 cases

Dice 1 (3): Dice 2 (4,5, & 6) i.e., 3 cases

Dice 1 (4): Dice 2 (5, & 6) i.e., 2 cases

Dice 1 (5): Dice 2 (6) i.e., 1 case

Hence, possible number of cases = 15/36 i.e., Option C.

Test: XAT Quant 2017 - Question 14
Save

An institute has 5 departments and each department has 50 students. If students are picked up randomly from all 5 departments to, form a committee, what should be the minimum number of students in the committee so that atleast one department should have representation of minimum 5 students?
Detailed Solution for Test: XAT Quant 2017 - Question 14
If we choose maximum 4 students from each department, there will be 20 students. So, 21st student will ensure at least one group has 5 representatives.

Test: XAT Quant 2017 - Question 15
Save

If N = (11p+7)(7q–2)(5r+1)(35) is a perfect cube, where p, q, r and s are positive integers, then the smallest value of p + q + r + s is:
Detailed Solution for Test: XAT Quant 2017 - Question 15
If N is perfect cube, then (p + 7), (q – 2), (r + 1) and (s) should be divided by 3 (11, 7, 5 and 3 being prime numbers). For smallest sum of p + q + r + s, p = 2, q = 2, r = 2 and s = 3 (all are positive integers) Answer = 9 (Option E).

Test: XAT Quant 2017 - Question 16
Save

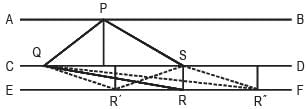
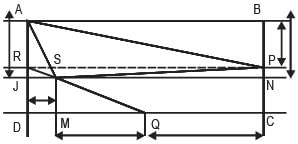
AB, CD and EF are three parallel lines, in that order. Let d1 and d2 be the distances from CD to AB and EF respectively. d1 and d2 are integers, where d1 : d2 = 2 : 1. P is a point on AB, Q and S are points on CD and R is a point on EF. If the area of the quadrilateral PQRS is 30 square units,

Q. what is the value of QR when value of SR is the least?
Detailed Solution for Test: XAT Quant 2017 - Question 16

The area of PQSR is 30 with heights of QPS and QRS in the proportions of 2 : 1. It is further given that heights are integers; it means that QR would be maximum for when value of d1 : d2 is lowest integer. The lowest possible integer value of d1 and d2 can be 1 and 2. For all other values of d1 and d2 (for example, 4 and 2, or 8 and 4), the value of QR will be lower. This implies, that values of d1 = 2 units and value of d2 = 1 unit.

For these values of d1 and d2; area of ∆QPS will be 20 and area of ∆QRS will be 10 (in proportion to the heights). The two triangles have same base: QS. Area of ∆QPS = 20

1/2 × QS × d1 = 20

1/2 × QS × 2 = 20

QS = 20

Further, the least possible value of SR = 1 (all other possible values of SRs will be greater than 1, as can be seen in ∆QR’S and ∆QR’S). Which means ∆QSR is a right-angle triangle in which:

QS2 + SR2 = QR2

20 × 20 + 1 × 1 = QR2

QR2 = √401

QR = slightly greater than 20

Test: XAT Quant 2017 - Question 17
Save

ABCD is a rectangle. P, Q and R are the midpoint of BC, CD and DA. The point S lies on the line QR in such a way that SR : QS = 1 : 3. The ratio of the triangle APS and rectangle ABCD is
Detailed Solution for Test: XAT Quant 2017 - Question 17

To get to the answer, we need to find area of APS. Let us assume the length of rectangle to be 16x and breadth to be 8y.

Therefore, area of rectangle is = 16x × 8y = 128xy

BP = PC = AR = RD = 4y, Similarly, DQ = QC = 8x

SQ = 3(SR) ⇒ MQ = 3(DM) = 6x ⇒ MD = 2x

Also, JD = 3RJ = 3y ⇒ AJ = 5y, JD = 3y, PN = RJ = y

Area of APS = Area of AJNB - Area of ∆AJS-Area of ∆ABPArea of ∆SPN, where AJS,

ABP and SPN are all right angled triangles.

Area of AJNB = 16x × 5y = 80xy Area of AJS = 1/2 × 2x × 5y = 5xy

Area of APB = 1/2 × 16x × 4y = 32xy

Area of SPN = 1/2 × y × 14x = 7xy

Area of APS = 80xy – 32xy – 7xy – 5xy = 36xy

Therefore, area of APS/Area of ABCD = 36xy/128xy = 36/128.

Test: XAT Quant 2017 - Question 18
Save

Study the data given in the caselet below and answer the questions that follow:

In an innings of a T20 cricket match (a team can bowl for 20 avers) 6 bowlers bowled from the fielding side, with a bowler allowed maximum of 4 overs. Only the three specialist bowlers bowled their full quota of 4 overs each, and the remaining 8 overs were shared among three non-specialist bowlers. The economy rates of four bowlers were6, 6, 7 and 9 respectively. (Economy rate is the total number of runs conceded by a bowler divided by the number of overs bowled by that bowler). This however, does not include the data of the best bowler (lowest economy rate) and the worst bowler (highest economy rate). The number of overs bowled and the economy rate of any bowler are in integers.

Read the two statements below: S1: The worst bowler did not bowl the minimum number of overs. S2: The best bowler is a specialist bowler.

Q. Which of the above statements or their combinations can help arrive at the minimum number of overs bowled by a non-specialist bowler?
Detailed Solution for Test: XAT Quant 2017 - Question 18
3, 3, 2 is the correct distribution. Other possible combinations will violate the conditions of maximum overs mentioned in the question. So, the question can be answered without using S1 and S2.

Test: XAT Quant 2017 - Question 19
Save

Study the data given in the caselet below and answer the questions that follow:

In an innings of a T20 cricket match (a team can bowl for 20 avers) 6 bowlers bowled from the fielding side, with a bowler allowed maximum of 4 overs. Only the three specialist bowlers bowled their full quota of 4 overs each, and the remaining 8 overs were shared among three non-specialist bowlers. The economy rates of four bowlers were6, 6, 7 and 9 respectively. (Economy rate is the total number of runs conceded by a bowler divided by the number of overs bowled by that bowler). This however, does not include the data of the best bowler (lowest economy rate) and the worst bowler (highest economy rate). The number of overs bowled and the economy rate of any bowler are in integers.

Read the two statements below: S1: The worst bowler did not bowl the minimum number of overs. S2: The best bowler is a specialist bowler.

Read the two statements below: S1. The economy rates of the specialist bowlers are lower than that of the non-specialist bowlers. S2. The cumulative runs conceded by the three non-specialist bowlers were 1 more than those conceded by the three specialist bowlers.

Q. Which of the above statements or their combinations can help arrive at the economy rate of the worst bowler?
Detailed Solution for Test: XAT Quant 2017 - Question 19
All the regular bowlers have lower economy rate. Further, these rates have to be in integers. Let the best economy rate be a. Worst is b.

According to S1: a < 6 and b > 9 and all the regular bowler’s economy rate is less than or equal to 6.

If we use S2, three possible conditions emerge:

Condition 1: If the worst bowler gets three overs 4 × a + 4 × 6 + 4 × 6 + 1 = 3 × 7 + 2 × 9 + 3 × b.

Solving this gives us an equation: 4 × a – 3 × b = –10.

Since both a and b have to be integers the only possible values of a and be are 5 and 10.

Condition 2: If worst bowler gets two overs but the bowlers with economy rates of nine and seven get three overs each: 4 × a + 48 + 1 = 21 + 27 + 2 × b, which gives us 4 5 a – 2 × b = –1. As, a and b are not integers, this possibility cannot be entertained.

Condition 3: If worst bowler gets three overs, but the bowler with economy of nine gets three overs and the bowler with economy rate of seven gets two overs: 4 × a + 48 + 1= 2 × 7 + 3 × 9 + 3 × b. Solving this should give us the equation 4 × a – 3 × b = –8 ⇒ 3b – 4a = 8. We get the integer solution in this case (b = 4 and a = 1), but this does not satisfy S1 and, therefore, cannot be entertained.

Hence, using only S2, we get two “integer” solutions, out of which one does not satisfy S1. So, we are left with only one possible solution (a = 5 and b = 10), if we use both S1(a < 6, and b > 9) and S2(cumulative runs scored…).

Test: XAT Quant 2017 - Question 20
Save

Study the paragraph below and answer the questions that follow:

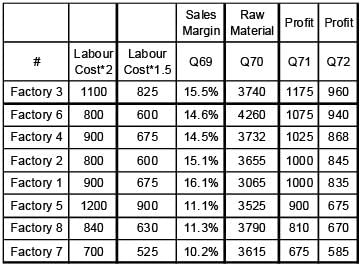
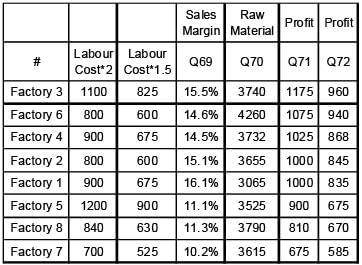
Abdul has 8 factories, with different capacities, producing boutique kurtas. In the production process, he incurs raw material, cost, selling cost (for packaging and transportation) and labour cost. These costs per kurta vary across factories. In all these factories, a worker takes 2 hours to produce a kurta. Profit per kurta is calculated by deducting raw material cost, selling cost and labour cost from the selling price (Profit = selling price – raw materials cost – selling cost – labour cost). Any other cost can be ignored.

Exhibit: Business Details of Abdul's 8 Factories

Q. Which of the following options is in decreasing order of raw materials cost?
Detailed Solution for Test: XAT Quant 2017 - Question 20

Test: XAT Quant 2017 - Question 21
Save

Study the paragraph below and answer the questions that follow:

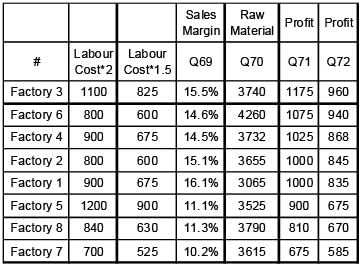
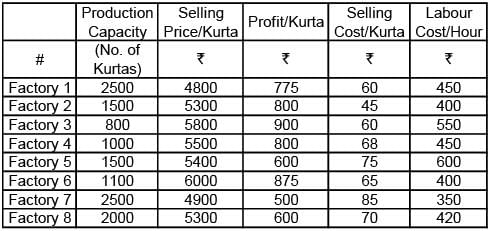
Abdul has 8 factories, with different capacities, producing boutique kurtas. In the production process, he incurs raw material, cost, selling cost (for packaging and transportation) and labour cost. These costs per kurta vary across factories. In all these factories, a worker takes 2 hours to produce a kurta. Profit per kurta is calculated by deducting raw material cost, selling cost and labour cost from the selling price (Profit = selling price – raw materials cost – selling cost – labour cost). Any other cost can be ignored.

Exhibit: Business Details of Abdul's 8 Factories

Q. Which of the factories listed in the options below has the lowest sales margin (sales margin = profit per kurta divided by selling price per kurta)?
Detailed Solution for Test: XAT Quant 2017 - Question 21

Test: XAT Quant 2017 - Question 22
Save

Study the paragraph below and answer the questions that follow:

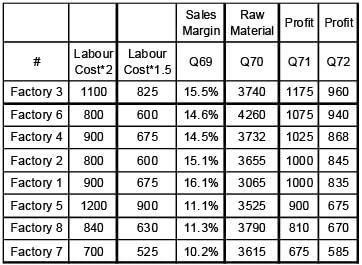
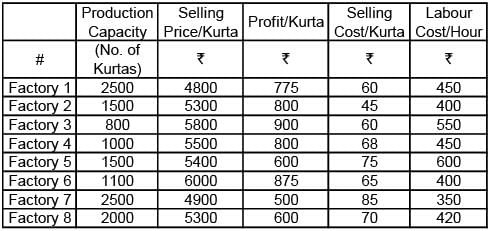
Abdul has 8 factories, with different capacities, producing boutique kurtas. In the production process, he incurs raw material, cost, selling cost (for packaging and transportation) and labour cost. These costs per kurta vary across factories. In all these factories, a worker takes 2 hours to produce a kurta. Profit per kurta is calculated by deducting raw material cost, selling cost and labour cost from the selling price (Profit = selling price – raw materials cost – selling cost – labour cost). Any other cost can be ignored.

Exhibit: Business Details of Abdul's 8 Factories

Abdul has received an order for 2,000 kurtas from a big retail chain. They will collect the finished pre-packaged kurtas directly from the factories, saving him the selling cost. To deliver this order, he can use multiple factories for production.

Q. Which of the following options will ensure maximum profit from this order?
Detailed Solution for Test: XAT Quant 2017 - Question 22

Test: XAT Quant 2017 - Question 23
Save

Study the paragraph below and answer the questions that follow:

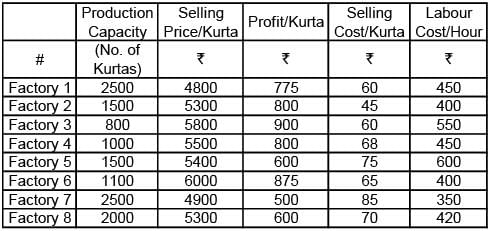
Abdul has 8 factories, with different capacities, producing boutique kurtas. In the production process, he incurs raw material, cost, selling cost (for packaging and transportation) and labour cost. These costs per kurta vary across factories. In all these factories, a worker takes 2 hours to produce a kurta. Profit per kurta is calculated by deducting raw material cost, selling cost and labour cost from the selling price (Profit = selling price – raw materials cost – selling cost – labour cost). Any other cost can be ignored.

Exhibit: Business Details of Abdul's 8 Factories

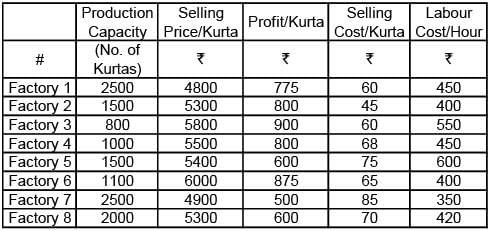
Abdul has introduced a new technology in all his factories. As a result, a worker needs just 1.5 hours to produce a kurta. If raw materials cost and selling cost remain the same,

Q. which of the factories listed in the options below will yield the highest profit per kurta?
Detailed Solution for Test: XAT Quant 2017 - Question 23

Test: XAT Quant 2017 - Question 24
Save

Analyse the graph below and answer the questions that follow:

The grid below captures relationships among seven personality dimensions: "extraversion", "true_arousal_plac", "true_arousal_caff', "arousal_plac", "arousal_caff', "performance_plac", and "performance_caff'. The diagonal represents histograms of the seven dimensions. Left of the diagonal represents scatterplots between the dimensions while the right of the diagonal represents quantitative relationships between the dimensions. The lines in the scatterplots are closest approximation of the points. The value of the relationships to the right of the diagonal can vary from –1 to +1, with –1 being the extreme linear negative relation and +1 extreme linear positive relation. (Axes of the graph are conventionally drawn).

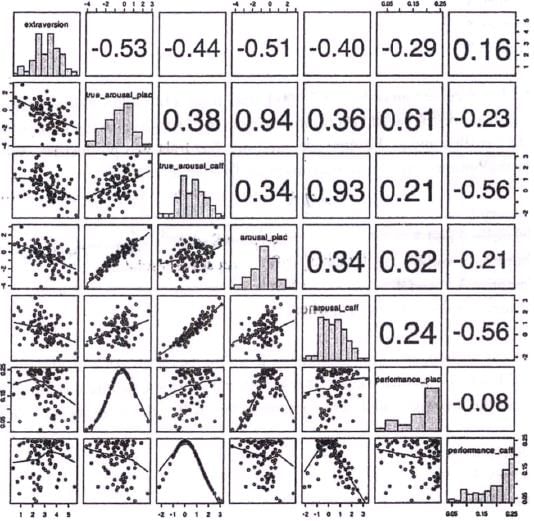
Q. Which of the following is true?
Detailed Solution for Test: XAT Quant 2017 - Question 24
We need to look at histogram to interpret the answer. The histogram for performance_caff and performance_plac is left skewed (most of data are on right side), which will shift median to right side compared to the mean. The situation is opposite in case of arousal_caff. Furthermore, arousal_plac‘s histogram is not symmetric and hence, there is no guarantee of its mean and median being equal. Hence, options B, C, D and E are incorrect and Option A is right

Test: XAT Quant 2017 - Question 25
Save

Analyse the graph below and answer the questions that follow:

The grid below captures relationships among seven personality dimensions: "extraversion", "true_arousal_plac", "true_arousal_caff', "arousal_plac", "arousal_caff', "performance_plac", and "performance_caff'. The diagonal represents histograms of the seven dimensions. Left of the diagonal represents scatterplots between the dimensions while the right of the diagonal represents quantitative relationships between the dimensions. The lines in the scatterplots are closest approximation of the points. The value of the relationships to the right of the diagonal can vary from –1 to +1, with –1 being the extreme linear negative relation and +1 extreme linear positive relation. (Axes of the graph are conventionally drawn).

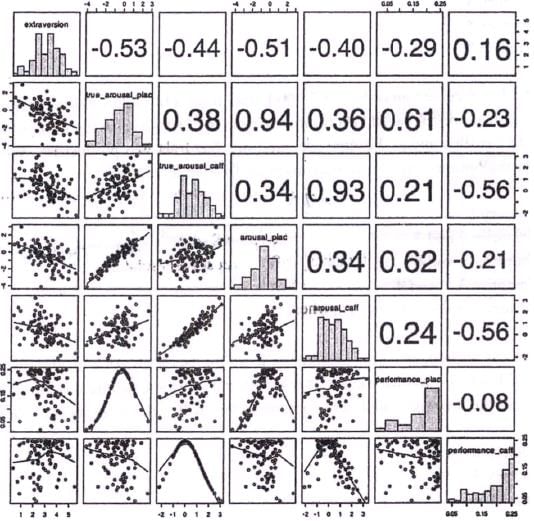
Q. Which of the scatterplots shows the weakest relationship?
Detailed Solution for Test: XAT Quant 2017 - Question 25
The weakest relationship should be away from “extreme values”, i.e. it should be the closest to zero. The closest relationship to zero, among the five options, is .16, which is between “extraverion” and “performance_caff”. Therefore, A is the right option.

Test: XAT Quant 2017 - Question 26
Save

Analyse the graph below and answer the questions that follow:

The grid below captures relationships among seven personality dimensions: "extraversion", "true_arousal_plac", "true_arousal_caff', "arousal_plac", "arousal_caff', "performance_plac", and "performance_caff'. The diagonal represents histograms of the seven dimensions. Left of the diagonal represents scatterplots between the dimensions while the right of the diagonal represents quantitative relationships between the dimensions. The lines in the scatterplots are closest approximation of the points. The value of the relationships to the right of the diagonal can vary from –1 to +1, with –1 being the extreme linear negative relation and +1 extreme linear positive relation. (Axes of the graph are conventionally drawn).

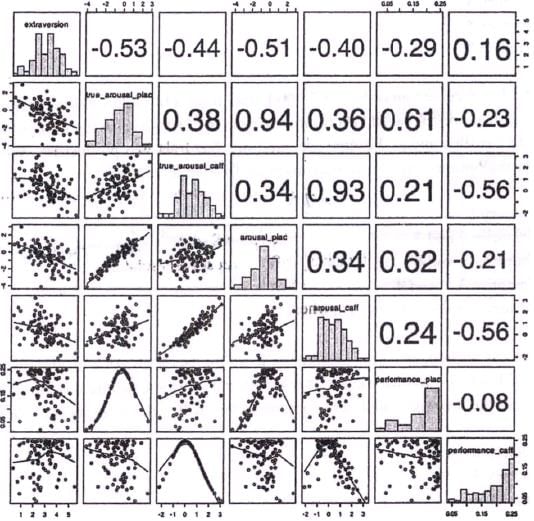
Q. In which of the following scatterplots, the value of one dimension can be used to predict the value of another, as accurately as possible?
Detailed Solution for Test: XAT Quant 2017 - Question 26
The question can be answerd by looking at the scatterplot, which is on the left-hand side of the diagonal. Option A is weak as the scatter is dispersed all over. Option B is very close, but some dispersion can be seen away from the “trend line”. The scatterplot in the option D is dispersed as well and hence it cannot be right answer. The scatterplot in the option C is the closest to the trend line and hence it should be the answer, though the relationship is weaker as compared to that in the option B (This is because it is curvilinear in shape, while relationship value assumes linearity).

Test: XAT Quant 2017 - Question 27
Save

Analyse the graph below and answer the questions that follow:

The grid below captures relationships among seven personality dimensions: "extraversion", "true_arousal_plac", "true_arousal_caff', "arousal_plac", "arousal_caff', "performance_plac", and "performance_caff'. The diagonal represents histograms of the seven dimensions. Left of the diagonal represents scatterplots between the dimensions while the right of the diagonal represents quantitative relationships between the dimensions. The lines in the scatterplots are closest approximation of the points. The value of the relationships to the right of the diagonal can vary from –1 to +1, with –1 being the extreme linear negative relation and +1 extreme linear positive relation. (Axes of the graph are conventionally drawn).

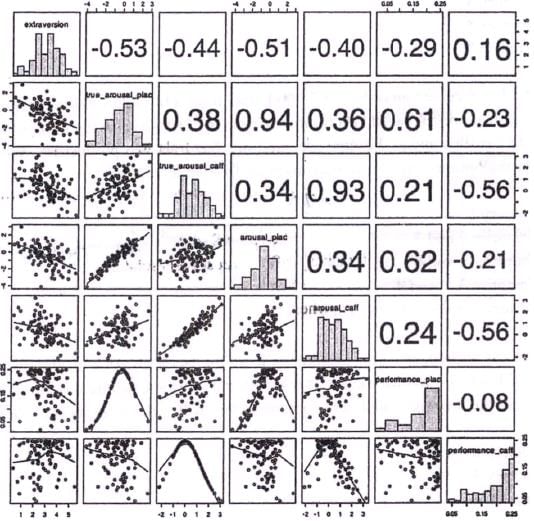
Q. Which of the following options is correct?
Detailed Solution for Test: XAT Quant 2017 - Question 27
Comparison between the visual pattern in the left side and the numbers in the right-hand side indicates Option B is the correct answer.
Information about Test: XAT Quant 2017 Page
In this test you can find the Exam questions for Test: XAT Quant 2017 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: XAT Quant 2017, EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for XAT Quant 2017

Find all the important questions for XAT Quant 2017 at EduRev.Get fully prepared for XAT Quant 2017 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the XAT Quant 2017 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of XAT Quant 2017 resources.

XAT Quant 2017 MCQs with Answers

Prepare for the XAT Quant 2017 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for XAT Quant 2017

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace XAT Quant 2017 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup