Triangles - Olympiad Level MCQ, Class 10 Mathematics - Class 10 MCQ
25 Questions MCQ Test - Triangles - Olympiad Level MCQ, Class 10 Mathematics
If the medians of a triangle are equal, then the triangle is:
The incentre of a triangle is determined by the:
The point of intersection of the angle bisectors of a triangle is :
A triangle PQR is formed by joining the mid-points of the sides of a triangle ABC. 'O' is the circumcentre of
ΔABC, then for ΔPQR, the point 'O' is :
If AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
In an equilateral ΔABC, if a, b and c denote the lengths of perpendiculars from A, B and C respectively on the opposite sides, then:
Any two of the four triangles formed by joining the midpoints of the sides of a given triangle are:
The internal bisectors of ∠B and ∠C of ΔABC meet at O. If ∠A = 80° then ∠BOC is :
The point in the plane of a triangle which is at equal perpendicular distance from the sides of the triangle is :
Incentre of a triangle lies in the interior of :
In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4 (AN2 + CM2) is equal to–
ABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BD/CD is equal to :
Let ABC be an equilateral triangle. Let BE . CA meeting CA at E, then (AB2 + BC2 + CA2) is equal to :
If D, E and F are respectively the mid-points of sides of BC, CA and AB of a ΔABC. If EF = 3 cm, FD =
4 cm, and AB = 10 cm, then DE, BC and CA respectively will be equal to :
In the right angle triangle ∠C = 90°. AE and BD are two medians of a triangle ABC meeting at F. The ratio
of the area of ΔABF and the quadrilateral FDCE is :
The bisector of the exterior ∠A of ΔABC intersects the side BC produced to D. Here CF is parallel to AD.
The diagonal BD of a quadrilateral ABCD bisects ∠B and ∠D, then:
Two right triangles ABC and DBC are drawn on the same hypotenuse BC on the same side of BC. If AC and
DB intersects at P, then
In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C
respectively. If AC = 5 cm and AD = 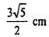 , find the length of CE:
, find the length of CE:
In a ΔABC, AB = 10 cm, BC = 12 cm and AC = 14 cm. Find the length of median AD. If G is the centroid,
find length of GA :
The three sides of a triangles are given. Which one of the following is not a right triangle?
In the figure AD is the external bisector of ∠EAC, intersects BC produced to D. If AB = 12 cm, AC = 8 cm
and BC = 4 cm, find CD.
In ΔABC, AB2 + AC2 = 2500 cm2 and median AD = 25 cm, find BC.
In the given figure, AB = BC and ∠BAC = 15°, AB = 10 cm. Find the area of ΔABC.
















