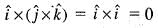Vector Calculus - 1 - IIT JAM MCQ
20 Questions MCQ Test - Vector Calculus - 1
For a scalar function  (x, y, z) = x2 + 3y2 + 2z2, the directional derivative at the point P( 1, 2, -1) is the direction of a vector
(x, y, z) = x2 + 3y2 + 2z2, the directional derivative at the point P( 1, 2, -1) is the direction of a vector 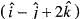 is
is
 (x, y, z) = x2 + 3y2 + 2z2, the directional derivative at the point P( 1, 2, -1) is the direction of a vector
(x, y, z) = x2 + 3y2 + 2z2, the directional derivative at the point P( 1, 2, -1) is the direction of a vector 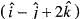 is
isUse the divergence theorem the value of 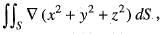 where, S is any closed surface enclosing volume V.
where, S is any closed surface enclosing volume V.
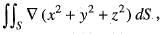 where, S is any closed surface enclosing volume V.
where, S is any closed surface enclosing volume V.Apply Stoke’s theorem, the value of 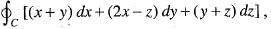 where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6) is
where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6) is
If 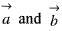 are to arbitrary vectors with magnitudes a and b respectively,
are to arbitrary vectors with magnitudes a and b respectively, 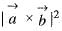 will be equal to
will be equal to
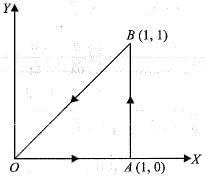
If 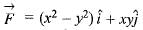 and curve C is the arc of the curve y = x3 from (0, 0 ) to (2, 8), then the value of
and curve C is the arc of the curve y = x3 from (0, 0 ) to (2, 8), then the value of 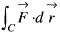
The value of 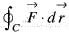 by Stoke’s theorem, where
by Stoke’s theorem, where 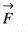
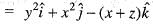 and C is the boundary of the triangle with vertices at ( 0 ,0 , 0 ) , ( 1 , 0 , 0 ) and ( 1 ,1 , 0 ) is
and C is the boundary of the triangle with vertices at ( 0 ,0 , 0 ) , ( 1 , 0 , 0 ) and ( 1 ,1 , 0 ) is
If 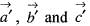 is the reciprocal system to the vectors
is the reciprocal system to the vectors 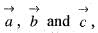 then the value of
then the value of 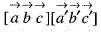 is
is
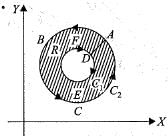
R is a closed planar region as shown by the shaded area in the figure below. Its boundary C consists of the circles C1 and C2.
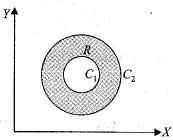
If 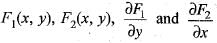 are all continuous everywhere in R, Green’s theorem states that
are all continuous everywhere in R, Green’s theorem states that
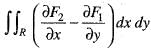
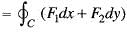
Which one of the following alternatives correctly depicts the direction of integration along C?
Use Gauss’s divergence theorem to find  where
where 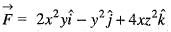 and S is the closed surface in the first octant bounded by y2 + z2 = 9 and x = 2.
and S is the closed surface in the first octant bounded by y2 + z2 = 9 and x = 2.
For the scalar field 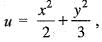 magnitude of the gradient at the point (1, 3) is
magnitude of the gradient at the point (1, 3) is


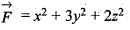
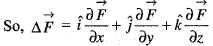
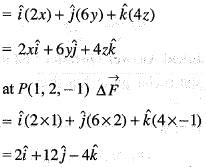
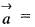
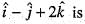
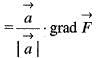
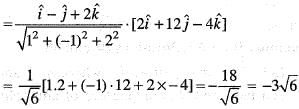

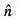 is an outward drawn unit normal vector to S.
is an outward drawn unit normal vector to S.

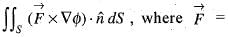
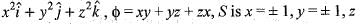
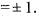
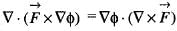
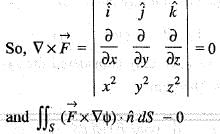
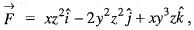 then the value of div
then the value of div 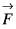 at the point (1, 1, -1) will be
at the point (1, 1, -1) will be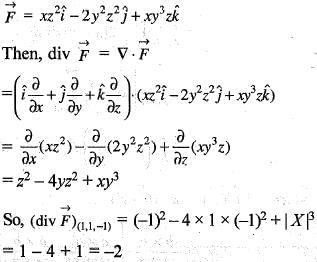
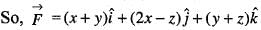
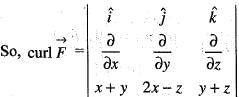

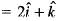
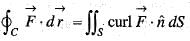
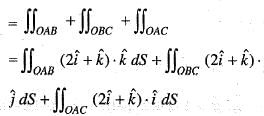
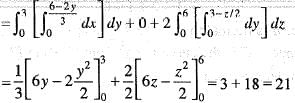
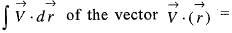
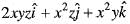 from the origin to the point P( 1,1,1) is
from the origin to the point P( 1,1,1) is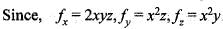
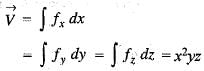
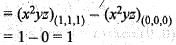
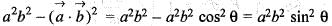
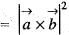
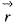 is
is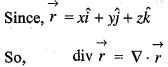
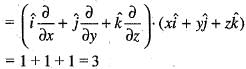
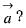
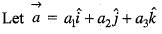
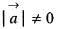
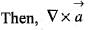

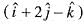 is
is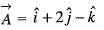
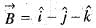
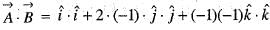
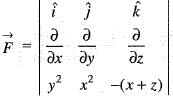
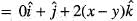
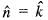
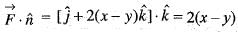
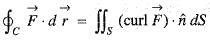
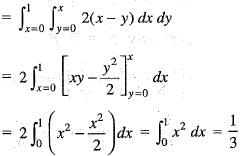
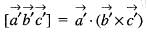
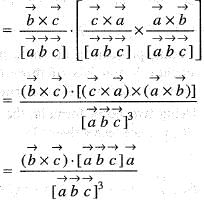
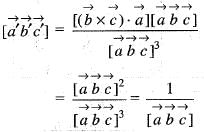
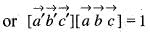
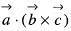 is equal to
is equal to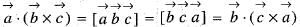
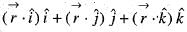 is
is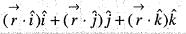
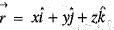
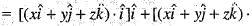
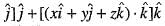
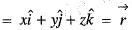
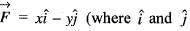 are unit vectors) is
are unit vectors) is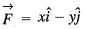
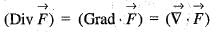
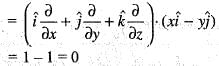
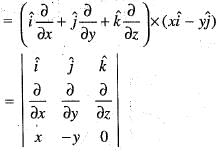
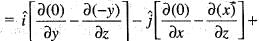

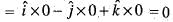
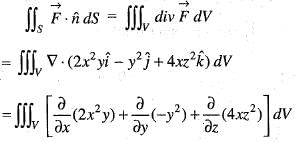
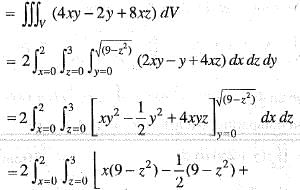
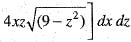
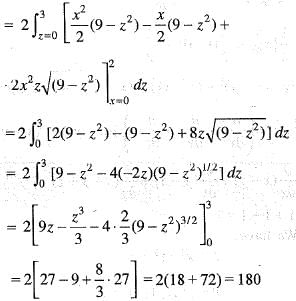
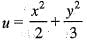
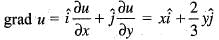
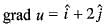
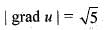
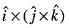 is equal to
is equal to