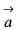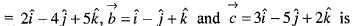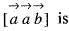Vector Calculus - 3 - IIT JAM MCQ
20 Questions MCQ Test - Vector Calculus - 3
If  is the unit outward drawn normal to any dosed surface S, then
is the unit outward drawn normal to any dosed surface S, then 
 is the unit outward drawn normal to any dosed surface S, then
is the unit outward drawn normal to any dosed surface S, then 
Let T (x, y, z) = xy2 + 2z – x2z2 be the temperature at the point (x, y, z). The unit vector in the direction in which the temperature decrease most rapidly at (1, 0, – 1) is
Let S be the oriented surface x2 + y2 + z2 = 1 with the unit normal n pointing outward. For the vector field F(x, y, z) = xi + yj + zk, the value of is
Let denote the force field on a particle traversing the path L from (0, 0, 0) to (1, 1, 1) along the curve of intersection of the cylinder y = x2 and the plane z = x. The work done by
is
A vector point function F is said to be solenoidal, if and only if
The work done in moving a particle in the force field F = 3x² i + (2xz - 9y) j+ zk along the line joining (0 , 0, 0) to (2 ,1, 3) is
If φ = sin (x + y + 2z) + x2 y3z, then curl grad φ is equal to
Consider the vector field , where a is a constant. If
, then the value of a is



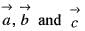 are coplanar vectors, then the value of
are coplanar vectors, then the value of 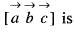
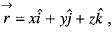 then the value of curl
then the value of curl  will be
will be at the point (1,-2,-1) is
at the point (1,-2,-1) is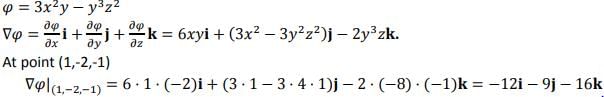
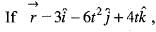 then the value of
then the value of 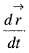 will be
will be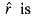
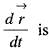
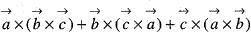 is
is