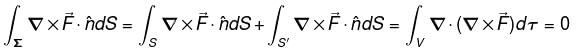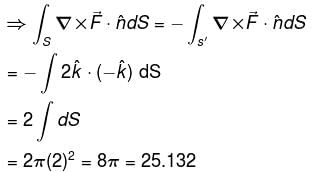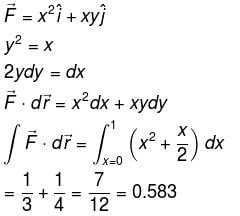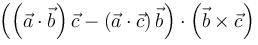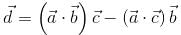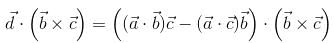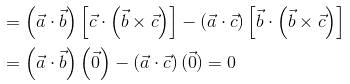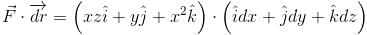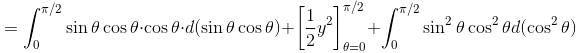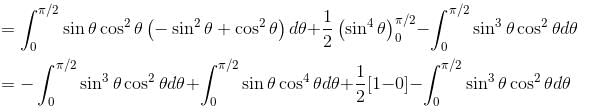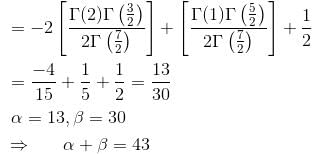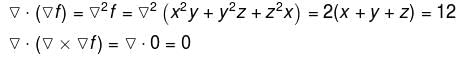Vector Calculus NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Vector Calculus NAT Level - 2
Evaluate 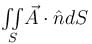 where
where 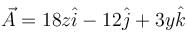 and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.
and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.
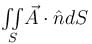 where
where 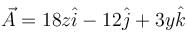 and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.
and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.Find the value of constant (a + b + c) so that the directional derivative of the function f = axy2 + byz + cz2x3 at the point (1, 2, –1) has maximum magnitude 64 in the direction parallel to y axis :
Evaluate the 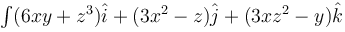 along the portion from path (1, 0, 1) to (3, 4, 5) of the curve C, which is the intersection of the surface z2 = x2 + y2 and z = y + 1.
along the portion from path (1, 0, 1) to (3, 4, 5) of the curve C, which is the intersection of the surface z2 = x2 + y2 and z = y + 1.
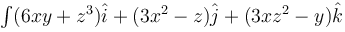 along the portion from path (1, 0, 1) to (3, 4, 5) of the curve C, which is the intersection of the surface z2 = x2 + y2 and z = y + 1.
along the portion from path (1, 0, 1) to (3, 4, 5) of the curve C, which is the intersection of the surface z2 = x2 + y2 and z = y + 1.The work done by the force 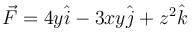 in moving a particle over circular path x2 + y2 = 1, z = 0 from (1, 0, 0) to (0, 1, 0) is :
in moving a particle over circular path x2 + y2 = 1, z = 0 from (1, 0, 0) to (0, 1, 0) is :
Let C be any curve x2 + y2 + z2 = 4, z > 0 and the vector field 
find out 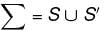
(Ans. upto three decimal places)
The value of the 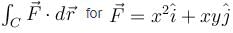 and C is the curve y2 = x joining (0, 0) to (1, 1) is (correct upto three decimal places)
and C is the curve y2 = x joining (0, 0) to (1, 1) is (correct upto three decimal places)
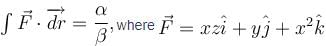 along the curve x = sin θ cos θ, y sin2 θ, z = cos θ with θ increasing from 0 to π/2. Find the value of α + β.
along the curve x = sin θ cos θ, y sin2 θ, z = cos θ with θ increasing from 0 to π/2. Find the value of α + β.
If f(x, y, z) = x2y + y2z + z2x for all (x, y, x) ∈ R3 and 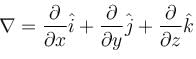 then the value of
then the value of 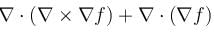 at (2, 2, 2) is :
at (2, 2, 2) is :


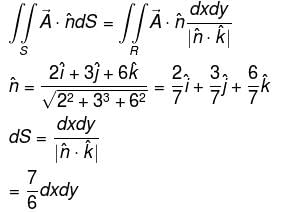
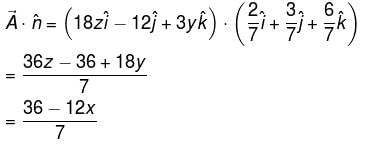
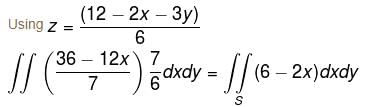
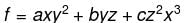
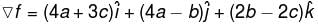 lies along y axis
lies along y axis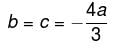
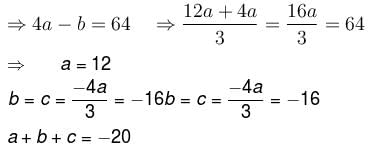

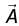 can be expressed as gradient of scalar function
can be expressed as gradient of scalar function 
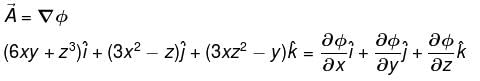
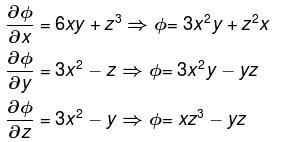
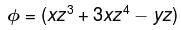
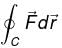 along the portion (1, 0, 1) to (3, 4, 5)
along the portion (1, 0, 1) to (3, 4, 5)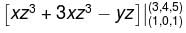
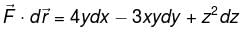

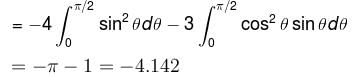
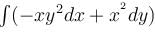 where C is the path shown in figure.
where C is the path shown in figure.
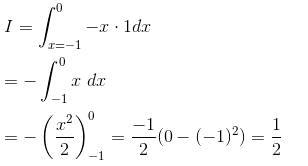
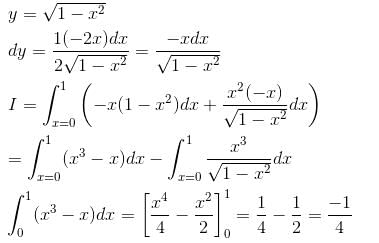
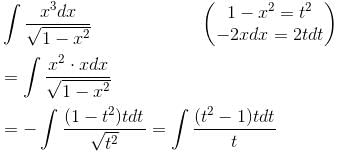
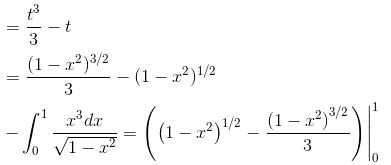
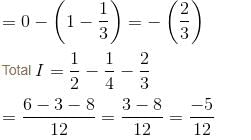

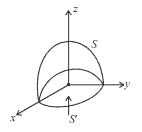
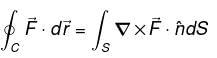
 consisting of S and S' i.e
consisting of S and S' i.e