Test: Area Of Parallelograms - Bank Exams MCQ
10 Questions MCQ Test NCERT Mathematics for Competitive Exams - Test: Area Of Parallelograms
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is:
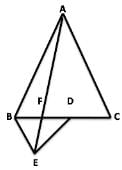
In the figure, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, then

In the figure, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, then
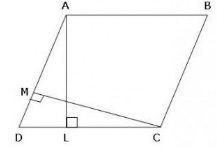
In parallelogram ABCD, AL ⊥ CD and CM ⊥ AD. If AL=20cm, CD = 12 cm, CM=8cm, then perimeter of the parallelogram is
PQRS is a trapezium in which PQ = 7 cm, PS = QR = 5 cm, RS = x cm and distance between PQ and RS is 4 cm. The area of trapezium is
A triangle and a rhombus are on the same base and between the same parallels. Then the ratio of area of triangle to that rhombus is:
ABCD is a parallelogram of area 100 cm2. AE is drawn perpendicular to BC and AF is drawn perpendicular to DC. If AE = 8 cm and AF is equal to 6.25 cm, then AB is
Parallelogram ABCD and rectangle ABEF are on the same base AB. If AB = 14 cm, BC = 12 cm, then the possible value for the perimeter of ABEF is
In the following figure, if ED = 10 cm, BG = 8 cm and BE = CD = 9 cm, then find the area of triangle CDF.
Find the area of quadrilateral ABCD, if AB || CD and AB = CD is as shown in figure :
|
276 docs|155 tests
|














