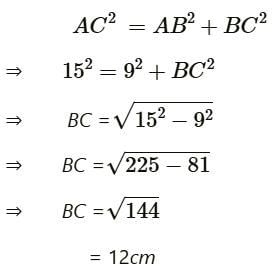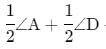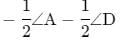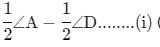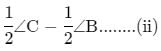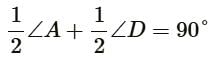Test: Quadrilaterals- 2 - Class 9 MCQ

P, Q, R are the mid- points of AB, BC, AC res, If AB = 10cm, BC = 8cm, AC = 12cm, Find the perimeter of △PQR.

In Triangle ABC which is right angled at B. Given that AB = 9cm, AC = 15cm and D, E are the mid-points of the sides AB and AC res. Find the length of BC?

Three Statements are given below:
(I) In a, Parallelogram the angle bisectors of 2 adjacent angles enclose a right angle.
(II) The angle bisector of a Parallelogram form a Rectangle.
(III) The Triangle formed by joining the mid-points of the sides of an isosceles triangle is not necessarily an isosceles triangle. Which is True?

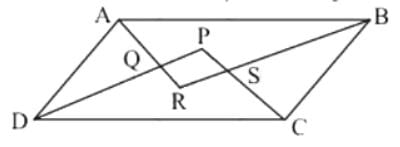
If APB and CQD are 2 parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form, square only if

If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a

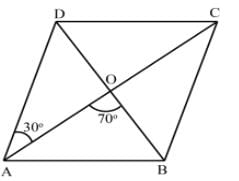
The Diagonals AC and BD of a Parallelogram ABCD intersect each other at the point O such that ∠DAC = 30^∘ and ∠AOB = 70^∘. Then, ∠DBC?

In Parallelogram ABCD, bisectors of angles A and B intersect each other at O. The measure of ∠AOB is

Three statements are given below:
(I) In a Rectangle ABCD, the diagonals AC bisects ∠A as well as ∠C.
(II) In a Square ABCD, the diagonals AC bisects ∠A as well as ∠C.
(III) In rhombus ABCD, the diagonals AC bisects ∠Aas well as ∠C.
Which is True?

D and E are the mid-points of the sides AB and AC of △ABC and O is any point on the side BC, O is joined to A. If P and Q are the mid-points of OB and OC res, Then DEQP is

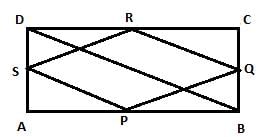
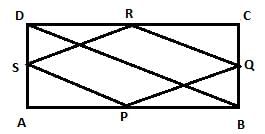
Given Rectangle ABCD and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA res. If length of a diagonal of Rectangle is 8cm, then the quadrilateral PQRS is a

In the given figure, ABCD is a Rhombus. Then, 

D and E are the mid-points of the sides AB and AC. Of △ABC. If BC = 5.6cm, find DE.

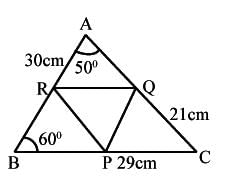
In a triangle P, Q and R are the mid-points of the sides BC, CA and AB res. If AC = 21cm, BC = 29cm and AB = 30cm, find the perimeter of the quadrilateral ARPQ?

The bisectors of the angles of a Parallelogram enclose a

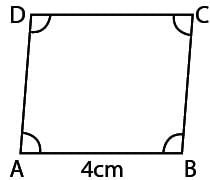
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.

In a Trapezium ABCD, if AB ║ CD, then (AC²+ BD²) = ?

In quadrilateral ABCD, ∠B=90^∘, ∠C−∠D = 60^∘ and ∠A−∠C−∠D = 10^∘. Find ∠A, ∠C and ∠D.

If a Quadrilateral ABCD,∠A = 90^∘ and AB = BC = CD = DA, Then ABCD is a

Rhombus is a quadrilateral

In △ABC, EF is the line segment joining the mid-points of the sides AB and AC. BC = 7.2cm, Find EF.

In the figure, ABCD is a rhombus, whose diagonals meet at 0. Find the values of x and y. 

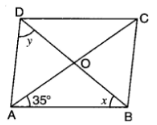
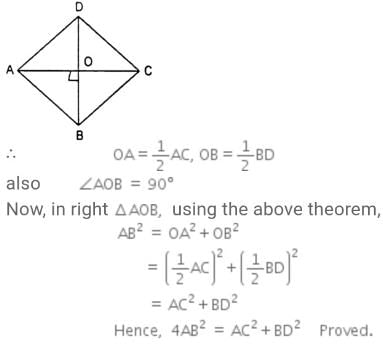
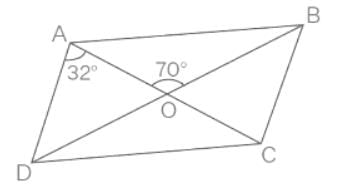
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32^∘ and ∠AOB = 70^∘ then, ∠DBC is equal to