परीक्षा: मात्रात्मक तर्क- 2 - RRB NTPC/ASM/CA/TA MCQ
20 Questions MCQ Test General Intelligence & Reasoning for RRB NTPC (Hindi) - परीक्षा: मात्रात्मक तर्क- 2
पाँच घंटे एक साथ बजना शुरू करते हैं और क्रमशः 6, 5, 7, 10 और 12 सेकंड के अंतराल पर बजते हैं। वे एक घंटे में एक साथ कितनी बार बजेंगे, शुरू होने वाले को छोड़कर?
एक बस शहर X से चलती है। बस में महिलाओं की संख्या पुरुषों की संख्या का आधा है। शहर Y में, 10 पुरुष बस से उतरते हैं और 5 महिलाएं चढ़ती हैं। अब, पुरुषों और महिलाओं की संख्या समान है। प्रारंभ में, बस में कितने यात्रियों ने प्रवेश किया?
A, B, C, D और E एक कार्ड का खेल खेलते हैं। A B से कहता है, "यदि तुम मुझे 3 कार्ड देते हो, तो तुम्हारे पास उतने ही होंगे जितने कि इस समय मेरे पास हैं, जबकि यदि D तुमसे 5 कार्ड लेता है, तो उसके पास E के जितने होंगे।" A और C के पास मिलकर E के पास मौजूद कार्ड की संख्या का दो गुना है। B और D के पास भी A और C के मिलकर रखे गए कार्ड के समान संख्या है। यदि उनके पास मिलाकर 150 कार्ड हैं, तो C के पास कितने कार्ड हैं?
एक किसान ने अपने चौकोर खेत के चारों ओर एक बाड़ बनाई। उसने चौकोर के प्रत्येक किनारे पर 27 बाड़ के खंभे इस्तेमाल किए। उसे कुल कितने खंभे की आवश्यकता थी?
एक शहर में, 40% वयस्क अशिक्षित हैं जबकि 85% बच्चे शिक्षित हैं। यदि वयस्कों और बच्चों का अनुपात 2 : 3 है, तो जनसंख्या का कितना प्रतिशत शिक्षित है?
A, B से तीन गुना बड़ा है। C, चार साल पहले A से दो गुना बड़ा था। चार साल बाद, A की उम्र 31 होगी। B और C की वर्तमान उम्र क्या है?
आज वरुण का जन्मदिन है। एक वर्ष बाद, वह 12 वर्ष पहले की तुलना में दो गुना बड़ा होगा। आज वरुण की उम्र क्या है?
एक पक्षी शिकारी से पूछा गया कि उसके पास बैग में कितने पक्षी हैं। उसने जवाब दिया कि उसमें सभी चिड़िया हैं सिवाय छह के, सभी कबूतर हैं सिवाय छह के, और सभी बतखें हैं सिवाय छह के। उसके पास बैग में कुल कितने पक्षी थे?
श्री जॉनसन को 300 पाउंड और सात सप्ताह के काम के लिए एक मुफ्त छुट्टी मिलनी थी। उन्होंने केवल 4 सप्ताह काम किया और 30 पाउंड और एक मुफ्त छुट्टी कमाई। छुट्टी की कीमत क्या थी?
इस गठन में तैरने वाले बतखों की सबसे छोटी संख्या क्या हो सकती है - एक बतख के सामने दो बतख, एक बतख के पीछे दो बतख और दो बतखों के बीच एक बतख?
तीन दोस्तों ने एक रेस्तरां में रात का खाना खाया। जब बिल मिला, तो अमिता ने जितना वेना ने भुगतान किया, उसका 2/3 भुगतान किया और वेना ने जितना तान्या ने भुगतान किया, उसका 1/2 भुगतान किया। वेना ने बिल का कितना भाग भुगतान किया?
एक कक्षा में, 20% सदस्य केवल दो कारें रखते हैं, 40% शेष सदस्यों के पास तीन कारें हैं और शेष सदस्य केवल एक कार रखते हैं। निम्नलिखित में से कौन सा वाक्य निश्चित रूप से सत्य है?
जब राहुल का जन्म हुआ, तो उसके पिता अपने भाई से 32 वर्ष बड़े थे और उसकी माँ अपनी बहन से 25 वर्ष बड़ी थी। यदि राहुल का भाई उससे 6 वर्ष बड़ा है और उसकी माँ अपने पिता से 3 वर्ष छोटी है, तो राहुल की बहन का जन्म के समय क्या उम्र थी?
एक निश्चित संख्या में घोड़े और उतनी ही संख्या में पुरुष कहीं जा रहे हैं। आधे मालिक अपने घोड़ों की पीठ पर हैं जबकि शेष लोग अपने घोड़ों को ले जाते हुए चल रहे हैं। यदि ज़मीन पर चलने वाले पैरों की संख्या 70 है, तो घोड़ों की संख्या कितनी है?
रवि का भाई उससे 3 वर्ष बड़ा है। उसके पिता की उम्र तब 28 वर्ष थी जब उसकी बहन का जन्म हुआ, जबकि उसकी माता की उम्र 26 वर्ष थी जब उसका जन्म हुआ। यदि उसकी बहन 4 वर्ष की थी जब उसका भाई पैदा हुआ, तो रवि के भाई के जन्म के समय उसके पिता और माता की उम्र क्रमशः क्या थी?
कक्षा में लड़कों की संख्या लड़कियों की संख्या से तीन गुना है। निम्नलिखित में से कौन सा संख्या कक्षा में बच्चों की कुल संख्या का प्रतिनिधित्व नहीं कर सकती?
एक भेड़पालक के पास 17 भेड़ें थीं। सभी नौ के अलावा मर गईं। उसके पास कितनी बचीं?
एक परिवार में, पिता ने केक का 1/4 हिस्सा लिया और उसके पास अन्य सदस्यों की तुलना में 3 गुना अधिक था। परिवार के सदस्यों की कुल संख्या क्या है?
तीन रंग के बक्सों - लाल, हरा और नीला में, 108 गेंदें रखी गई हैं। हरे और लाल बक्सों में मिलाकर गेंदों की संख्या नीले बक्से में गेंदों की संख्या की तुलना में दोगुनी है और नीले बक्से में गेंदों की संख्या लाल बक्से में गेंदों की संख्या की तुलना में दोगुनी है। हरे बक्से में कितनी गेंदें हैं?
एक क्रिकेट मैच में, पांच बल्लेबाजों A, B, C, D और E ने औसतन 36 रन बनाए। D ने E से 5 रन अधिक बनाए; E ने A से 8 रन कम बनाए; B ने D और E के मिलाकर बनाए गए रन के बराबर बनाए; और B और C ने मिलकर 107 रन बनाए। E ने कितने रन बनाए?
|
127 docs|197 tests
|
|
127 docs|197 tests
|




 x + 1 = 2x - 24
x + 1 = 2x - 24  x = 25।
x = 25।
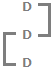


 6R = 108
6R = 108  R = 18.
R = 18.