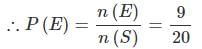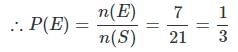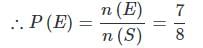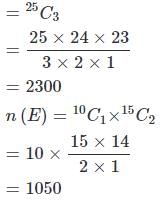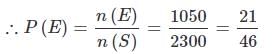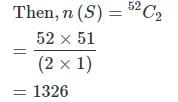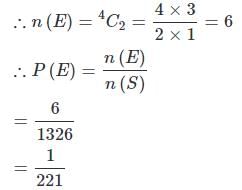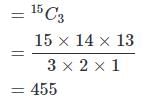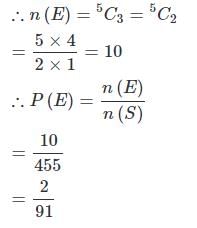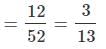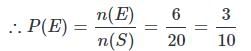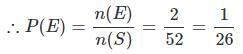परीक्षा: संभावना सिद्धांत - 2 - SSC CGL MCQ
10 Questions MCQ Test - परीक्षा: संभावना सिद्धांत - 2
टिकट संख्या 1 से 20 तक मिलाए गए हैं और फिर एक टिकट यादृच्छिक रूप से खींची जाती है। वह टिकट खींचने की संभावना क्या है जिसका नंबर 3 या 5 का गुणांक है?
एक डिब्बे में 8 लाल, 7 नीले और 6 हरे गेंदें हैं। एक गेंद को यादृच्छिक रूप से उठाया जाता है। यह संभावना क्या है कि यह न तो लाल है और न ही हरा?
तीन निष्पक्ष सिक्के उछाले जाते हैं। अधिकतम दो सिर (हेड्स) प्राप्त करने की संभावना क्या है?
एक कक्षा में 15 लड़के और 10 लड़कियाँ हैं। तीन छात्रों का यादृच्छिक रूप से चयन किया जाता है। 1 लड़की और 2 लड़कों का चयन होने की संभावना क्या है?
52 पत्तों के एक पैक से, दो पत्ते एक साथ यादृच्छिक रूप से खींचे जाते हैं। दोनों पत्ते राजाओं होने की संभावना क्या है?
एक बैग में 4 सफेद, 5 लाल और 6 नीले गेंदें हैं। बैग से यादृच्छिक रूप से तीन गेंदें खींची जाती हैं। संभावना कि वे सभी लाल हों, क्या है?
52 पत्तों के एक पैक से एक पत्ता यादृच्छिक रूप से निकाला जाता है। निकाले गए पत्ते का एक फेस कार्ड (जैक, रानी और राजा केवल) होने की संभावना क्या है?
1 से 20 तक के टिकट एक साथ मिलाए जाते हैं और फिर एक टिकट यादृच्छिक रूप से निकाला जाता है। उस टिकट के निकलने की संभावना क्या है जो 3 का गुणांक है?
एक बर्तन में 6 लाल, 4 नीले, 2 हरे और 3 पीले मार्बल हैं। यदि 4 मार्बल यादृच्छिक रूप से उठाए जाते हैं, तो उनमें से कम से कम एक नीला होने की संभावना क्या है?
52 पत्तों के एक पैक में से एक पत्ता निकाला जाता है। क्लब की रानी या हृदय का राजा पाने की संभावना क्या है?