MCQ: ऊँचाई और दूरी - 2 - RRB NTPC/ASM/CA/TA MCQ
15 Questions MCQ Test Mathematics for RRB NTPC (Hindi) - MCQ: ऊँचाई और दूरी - 2
एक व्यक्ति जो एक ऊर्ध्वाधर अवलोकन टॉवर के शीर्ष पर है, एक कार को समान गति से उसकी ओर आते हुए देखता है। यदि इसमें 10 मिनट लगते हैं कि अवनति का कोण 45° से 60° में बदल जाए, तो इसके बाद कार अवलोकन टॉवर तक पहुँचने में कितनी जल्दी पहुँचेगी?
दो जहाज समुद्र में एक灯टॉवर के दो किनारों पर चल रहे हैं।灯टॉवर के शीर्ष का ऊँचाई कोण जहाजों से क्रमशः 30° और 45° है। यदि灯टॉवर की ऊँचाई 100 मीटर है, तो दोनों जहाजों के बीच की दूरी क्या है?
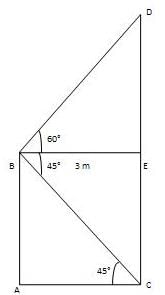
10 मीटर ऊँचे भवन के सर्वोच्च बिंदु से, टॉवर के सर्वोच्च बिंदु का पृष्ठ भाग 60° है और उसके पैर का पृष्ठ भाग 45° है, टॉवर की ऊँचाई ज्ञात करें। (मान लीजिए कि √3 = 1.732)
एक आदमी जो बिंदु P पर खड़ा है, एक टॉवर के शीर्ष को देख रहा है, जो आदमी की आंखों के साथ 30º का ऊँचाई का कोण बनाता है। आदमी टॉवर की ओर कुछ दूरी तक चलता है ताकि वह इसके शीर्ष को देख सके और ऊँचाई का कोण 60º हो जाता है। टॉवर के आधार और बिंदु P के बीच की दूरी क्या है?
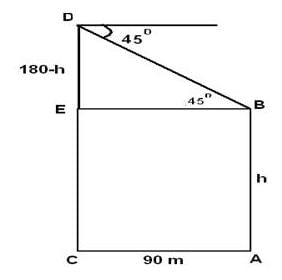
दो टावरों के बीच क्षैतिज दूरी 90 मीटर है। दूसरे टावर के शीर्ष से पहले टावर के शीर्ष की कोणीय अवसाद 45 डिग्री है, जो कि 180 मीटर ऊँचा है। तब पहले टावर की ऊँचाई क्या होगी?
जब एक पेड़ की छाया की लंबाई पेड़ की ऊँचाई का √3 गुणा होती है, तो सूर्य का उदय कोण है:
एक आदमी टॉवर के शीर्ष से एक नाव को देख रहा है जो टॉवर से दूर जा रही है। जब नाव टॉवर से 75 मीटर की दूरी पर होती है, तो नाव का दृष्टिकोन का कोण 60° होता है। 10 सेकंड बाद, दृष्टिकोन का कोण 45° हो जाता है। यदि मान लिया जाए कि नाव शांत पानी में चल रही है, तो नाव की अनुमानित गति क्या होगी?
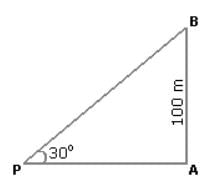
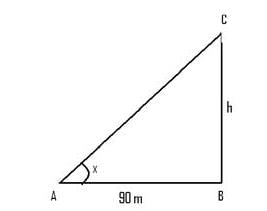
समतल भूमि पर बिंदु P से, शीर्ष टॉवर का उन्नयन कोण 30º है। यदि टॉवर की ऊँचाई 100 मीटर है, तो बिंदु P से टॉवर के पैर तक की दूरी क्या होगी?
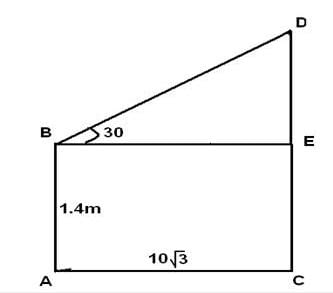
एक पर्यवेक्षक की ऊँचाई 1.4 मीटर है और वह एक टॉवर से 10√3 मीटर की दूरी पर है। उसके आंखों से टॉवर के शीर्ष की ओर उठने का कोण 60° है। टॉवर की ऊँचाई क्या है?
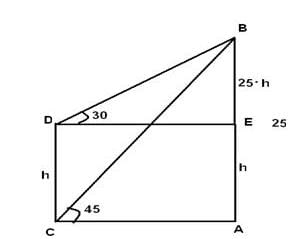
25 मीटर ऊँचे टॉवर की चोटी इलेक्ट्रिक पोल के नीचे से 45 डिग्री का ऊँचाई कोण बनाती है और पोल की चोटी से 30 डिग्री का ऊँचाई कोण बनाती है। इलेक्ट्रिक पोल की ऊँचाई ज्ञात करें।
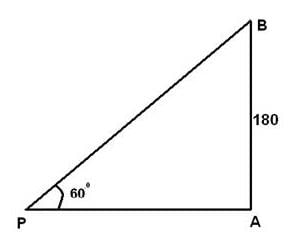
एक स्तर भूमि पर बिंदु P से, शीर्ष टॉवर का ऊर्ध्वाधर कोण 60° है। यदि टॉवर की ऊँचाई 180 मीटर है, तो बिंदु P की टॉवर के पैर से दूरी क्या होगी?
दो टावरों की ऊँचाई 90 मीटर और 45 मीटर है। उनके शीर्षों को जोड़ने वाली रेखा क्षैतिज के साथ 45 डिग्री का कोण बनाती है, तो दोनों टावरों के बीच की दूरी क्या है?
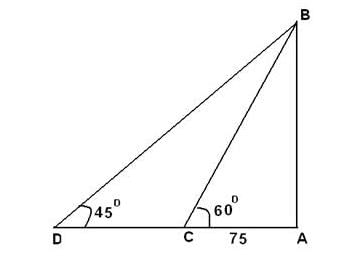
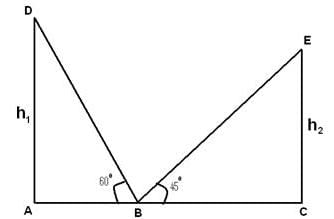
दो ऊर्ध्वाधर टावरों के शीर्षों के ऊँचाई के कोण, जो टावरों के आधार के बीच के मध्य बिंदु से देखे गए हैं, 45° और 60° हैं। टावरों की ऊँचाई का अनुपात क्या है?
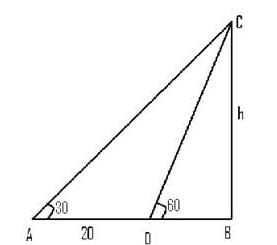
समतल भूमि पर, एक टॉवर के शीर्ष का ऊँचाई का कोण 30° है। 20 मीटर निकट जाने पर, ऊँचाई का कोण 60° हो जाता है। फिर टॉवर की ऊँचाई क्या है?
एक बिंदु से टॉवर के ऊँचाई का कोण 90 मीटर है, जो cot-1(4/5) है। फिर टॉवर की ऊँचाई क्या है?
|
142 videos|172 docs|185 tests
|


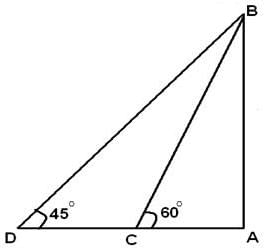
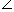 ACB = 30° और
ACB = 30° और 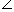 ADB = 45°।
ADB = 45°।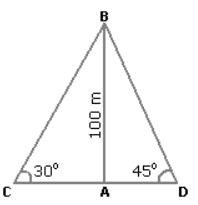
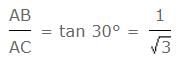
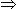

 ACB = heta;.
ACB = heta;. cot
cot  heta = 30º.
heta = 30º.