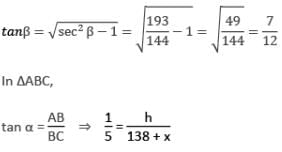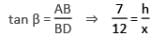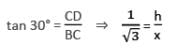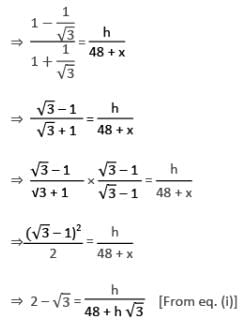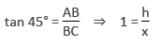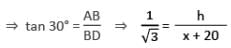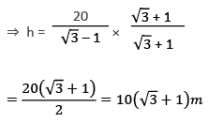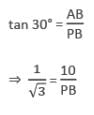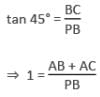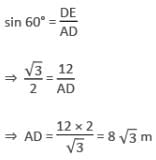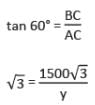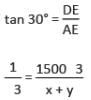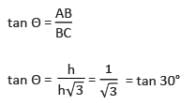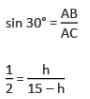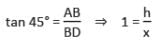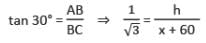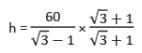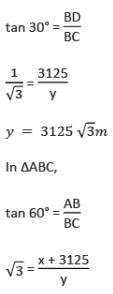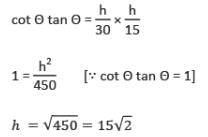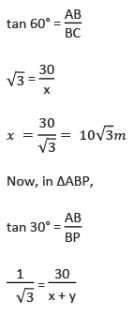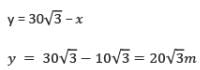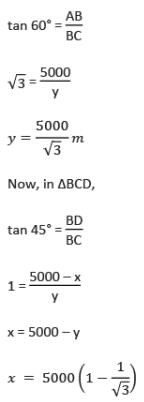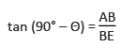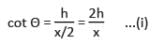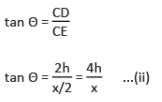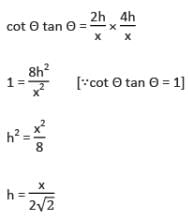Explore Exams
Login Signup
Sign in Open App
RRB NTPC/ASM/CA/TA Exam  >  RRB NTPC/ASM/CA/TA Tests  >  Mathematics for RRB NTPC (Hindi)  >  MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - RRB NTPC/ASM/CA/TA MCQ

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - RRB NTPC/ASM/CA/TA MCQ


Test Description

15 Questions MCQ Test Mathematics for RRB NTPC (Hindi) - MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 questions and answers have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus.The MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 MCQs are made for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 below.
Solutions of MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 questions in English are available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 solutions in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics, notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. Attempt MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 | 15 questions in 15 minutes | Mock test for RRB NTPC/ASM/CA/TA preparation | Free important questions MCQ to study Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA Exam | Download free PDF with solutions
MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 1
Save

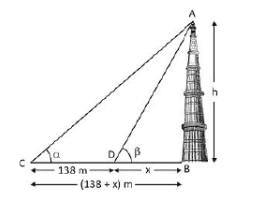
एक स्मारक के आधार के माध्यम से एक क्षैतिज रेखा पर एक बिंदु पर, स्मारक के शीर्ष के ऊर्ध्वाधर कोण का मूल्यांकन किया गया है, जिसका टेंजेंट 1/5 है। स्मारक की ओर 138 मीटर चलने पर ऊर्ध्वाधर कोण का सेकेंट √(193) / 12 पाया गया है। स्मारक की ऊँचाई (मीटर में) क्या है?

Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 1


दिया गया है, चलने की दूरी, CD = 138 मीटर
मान लें, स्मारक की ऊँचाई, AB = h मीटर
BD = x मीटर, ∠ACB = α और ∠ADB = β

∴ BC = CD + BD = (138 + x) मीटर
हमें पता है कि,

x = 5h – 138 ...(i)
अब, ΔABD में,

⇒ 7x = 12h
⇒ 7(5h – 138) = 12h [समीकरण (i) से]
⇒ 35h – 966 = 12h ⇒ 23h = 966 ⇒ h = 42 मीटर
∴ स्मारक की ऊँचाई 42 मीटर है।
इसलिए, विकल्प C सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 2
Save

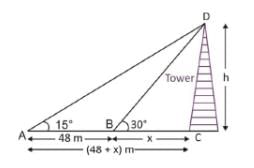
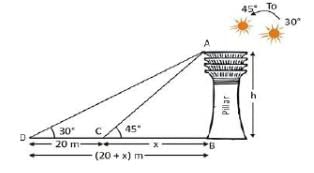
एक टॉवर के शीर्ष का ऊँचाई कोण दो बिंदुओं A और B से है, जो टॉवर के पैर के क्षैतिज रेखा पर स्थित हैं, क्रमशः 15° और 30° हैं। यदि A और B टॉवर के एक ही तरफ हैं और AB = 48 मीटर है, तो टॉवर की ऊँचाई क्या होगी?

Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 2

दी गई जानकारी के अनुसार, AB = 48 मीटर
मान लें, टॉवर की ऊँचाई, CD = h मीटर
और, BC = x मीटर
इसलिए, AC = AB + BC = (48 + x) मीटर
ΔBCD में,
x = h √3 ...(i)
अब, ACD में,
h = 96 + 2h √3 – 48 √3 – 3h
4h – 2h √3 = 48(2 – √3)
2h(2 – √3) = 48(2 – √3)
h = 24 मीटर
इसलिए, टॉवर की ऊँचाई 24 मीटर है।
इसलिए, विकल्प B सही है।

Clear all your doubts with EduRev
MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 3
Save

यदि सूर्य के उर्ध्वाधर कोण में परिवर्तन 30° से 45° होता है, तो एक स्तंभ की छाया की लंबाई 20 मीटर कम हो जाती है। स्तंभ की ऊँचाई है

Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 3


चलो, स्तंभ की ऊँचाई, AB = h मीटर मान लेते हैं।
जब सूर्य का उन्नति कोण 30° था, तब स्तंभ की छाया की लंबाई BD थी।
और, जब सूर्य का उन्नति कोण 45° है, तब स्तंभ की छाया की लंबाई BC = x मीटर (मान लेते हैं)।
जब सूर्य 30° से 45° की ओर बढ़ता है, तब स्तंभ की छाया की लंबाई घटती है CD = 20 (दिया गया है)।
अतः BD = BC + CD = (x + 20) मीटर।
ΔABC में,

⇒ h = x ...(i)
अब, ΔABD में,

⇒ h √3 = x + 20
⇒ h √3 = h + 20 [समीकरण (i) से]
⇒ h (√3 – 1) = 20

अतः स्तंभ की ऊँचाई 10 (√3 + 1) मीटर है।
इसलिए, विकल्प D सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 4
Save

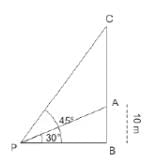
भूमि पर एक बिंदु P से 10 मीटर ऊंची इमारत की चोटी का ऊर्ध्वाधर कोण 30° है। इमारत की चोटी पर एक ध्वज फहराया गया है और P से ध्वज ध्वजस्तंभ की चोटी का ऊर्ध्वाधर कोण 45° है। ध्वजस्तंभ की लंबाई ज्ञात कीजिए। (मान लीजिए √3 = 1.732)
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 4


AC = झंडा, AB = भवन = 10 मीटर
∠APB = 30°; ∠CPB = 45°
Δ APB में,

⇒ PB = 10 √3 मीटर
ΔPBC में,

⇒ PB = AB + AC ⇒ 10 √3 = 10 + AC
⇒ AC = 10 √3 – 10
⇒ 10(√3 – 1) मीटर = 10(1.732 – 1) मीटर
= 10 × 0.732 = 7.32 मीटर।
इसलिए, विकल्प D सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 5
Save

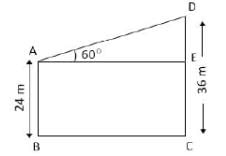
24 मीटर और 36 मीटर ऊँचाई वाले दो पोलों के शीर्ष को एक तार से जोड़ा गया है। यदि तार क्षैतिज के साथ 60° का कोण बनाता है, तो तार की लंबाई क्या होगी?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 5


DE = 36 - 24 = 12 मीटर
Δ ADE से,

इसलिए, विकल्प B सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 6
Save

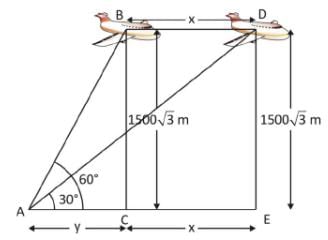
जमीन पर एक बिंदु से विमान का उन्नयन कोण 60° है। 15 सेकंड की उड़ान के बाद, उन्नयन 30° में बदल जाता है। यदि विमान की ऊँचाई 1500√3 मीटर है, तो विमान की गति ज्ञात करें।
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 6

दी गई जानकारी के अनुसार, विमान की ऊँचाई, BC = 1500 √3 मीटर है।
मान लें कि विमान ने 15 सेकंड में दूरी BD = x मीटर तय की।
और, AC = y मीटर है।
इसलिए, AE = CE + AC = (x + y) मीटर है।
ΔABC में,

y = 1500 मीटर है।
अब, ΔADE में,

x + y = 4500 है।
x + 1500 = 4500, x = 3000 मीटर है।
इसलिए, विमान ने 15 सेकंड में 3000 मीटर की दूरी तय की।
इसलिए, गति = 3000/15 = 200 मीटर/सेकंड है।
इसलिए, विकल्प A सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 7
Save

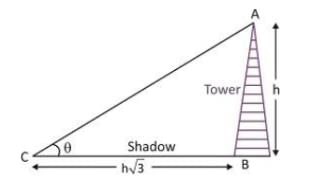
एक टॉवर की छाया उसकी ऊँचाई का √3 गुना है। तो टॉवर के शीर्ष का ऊँचाई का कोण क्या होगा?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 7


मान लीजिए, टॉवर की ऊँचाई, AB = h मीटर
और, ऊँचाई का कोण = Θ
फिर, टॉवर की छाया, BC = h√3 मीटर
ΔABC में,

Θ = 30°
इसलिए, विकल्प B सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 8
Save

एक 15 फीट ऊँचा लंबवत खंभा एक निश्चित ऊँचाई पर टूट जाता है और इसका ऊपरी भाग, जो पूरी तरह से अलग नहीं हुआ है, जमीन पर 30° के कोण पर मिलता है। उस ऊँचाई को खोजें जहाँ खंभा टूटा है।
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 8


\पोस्ट की कुल ऊँचाई = AB + AC = 15 फीट
\मान लें, पोस्ट बिंदु A पर टूटी है, इसलिए AB = h
\और, AC = 15 – AB = (15 – h) फीट
\ΔABC में,
\
\15 – h = 2h
\3h = 15
\h = 5 फीट
\इसलिए, विकल्प B सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 9
Save

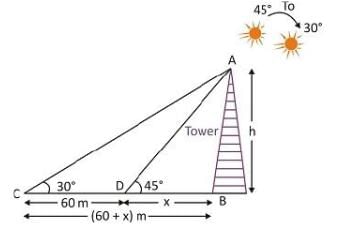
जब सूर्य की ऊँचाई 45° से 30° तक बदलती है, तो टॉवर की छाया 60 मीटर लंबी हो जाती है। तब टॉवर की ऊँचाई क्या होगी?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 9


मान लेते हैं, टॉवर की ऊँचाई, AB = h मीटर।
जब सूर्य की ऊँचाई का कोण 45° था, तब टॉवर की छाया की लंबाई BD = x (मान लेते हैं)।
जब सूर्य का कोण 45° से 30° तक बदलता है, तब टॉवर की छाया की लंबाई बढ़ जाती है CD = 60 मीटर (दी गई)।
और, जब सूर्य का ऊँचाई का कोण 30° होता है, तब टॉवर की छाया की लंबाई BC = CD + BD = (60 + x) मीटर होती है।
ΔABD में,

h = x
अब, ΔABC में,

h√3 - x = 60
h√3 - h = 60 [∵ h = x]
h(√3 - 1) = 60

= 30(√3 + 1) मीटर
इसलिए, विकल्प C सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 10
Save

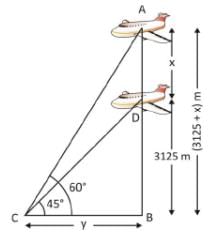
एक विमान जब जमीन से 3125 मीटर की ऊँचाई पर उड़ रहा होता है, तब वह एक अन्य विमान के ठीक नीचे से गुजरता है, जब जमीन पर एक ही बिंदु से दोनों विमानों का ऊर्ध्वाधर कोण क्रमशः 30° और 60° होता है। उस क्षण में दोनों विमानों के बीच की दूरी है
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 10


दिया गया है, एक विमान की ऊँचाई जमीन से, BD = 3125 मीटर
मान लें, विमानों के बीच की दूरी, AD = x मीटर
और, BC = y मीटर
अतः AB = AD + BD = (3125 + x) मीटर
ΔBCD में,

y√3 = x + 3125
3125√3 × √3 = x + 3125
x = 9375 – 3125 = 6250 मीटर
अतः विमानों के बीच की दूरी 6250 मीटर है।
इसलिए, विकल्प D सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 11
Save

दो ऊर्ध्वाधर पोलों के बीच की दूरी 60 मीटर है। एक पोल की ऊँचाई दूसरी पोल की ऊँचाई की दोगुनी है। पोलों के शीर्ष का उन्नति कोण उनके आधार के बीच के मध्य बिंदु से एक दूसरे के पूरक हैं। पोलों की ऊँचाई क्या है?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 11

दी गई जानकारी के अनुसार, BC = 60 मीटर,
E BC का मध्य बिंदु है।
तदनुसार BE = EC = 30 मीटर
मान लें कि पोल AB की ऊँचाई = h मीटर है,
तदनुसार पोल CD की ऊँचाई = 2h मीटर है।
और ∠AEB और ∠DEC पूरक हैं।
तदनुसार ∠AEB = (90° - Θ) और ∠DEC = Θ।
ΔABE में,
अब, ΔCDE में,
दोनों समीकरण (i) और (ii) को गुणा करने पर,
तदनुसार पोल AB की ऊँचाई = h = 15 √2 मीटर है।
और पोल CD की ऊँचाई = 2h = 2 × 15 √2 = 30 √2 मीटर है।
इसलिए, विकल्प D सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 12
Save

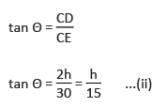
एक आदमी P बिंदु पर खड़ा है और एक टॉवर के शीर्ष को देख रहा है, जो 30° का ऊर्ध्वाधर कोण बनाता है। आदमी कुछ दूरी तय करता है टॉवर की ओर और फिर उसका ऊर्ध्वाधर कोण 60° हो जाता है। यदि टॉवर की ऊँचाई 30 मीटर है, तो उसकी चलने की दूरी कितनी है?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 12


दी गई जानकारी के अनुसार, टॉवर की ऊँचाई, AB = 30 मीटर है।
मान लें, आदमी ने जो दूरी तय की, वह CP = y मीटर है।
और BC = x मीटर है।
∴ BP = BC + CP = (x + y) मीटर।
ΔABC में,


इसलिए, विकल्प A सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 13
Save

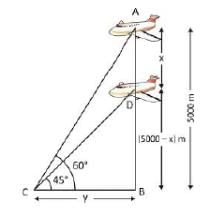
एक हवाई जहाज़ जब जमीन से 5000 मीटर की ऊँचाई पर उड़ रहा होता है, तब वह एक अन्य हवाई जहाज़ के ठीक ऊपर से गुजरता है, जब जमीन पर एक ही बिंदु से दोनों हवाई जहाज़ों के लिए ऊँचाई के कोण क्रमशः 60° और 45° होते हैं। उस क्षण में हवाई जहाज़ों के बीच ऊर्ध्वाधर दूरी क्या है?
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 13


दी गई जानकारी के अनुसार, हवाई जहाज़ की ऊँचाई जमीन से, AB = 5000 मीटर,
मान लीजिए, हवाई जहाज़ों के बीच की दूरी, AD = x मीटर
और, BC = y मीटर
तो, BD = AB – AD = (5000 – x) मीटर
ΔABC में,

इसलिए, विकल्प C सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 14
Save

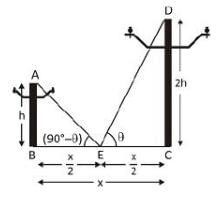
दो पोल x मीटर की दूरी पर हैं और इनमें से एक की ऊँचाई दूसरी की ऊँचाई का दो गुना है। यदि उनके पैरों को जोड़ने वाली रेखा के मध्य बिंदु से एक पर्यवेक्षक उनके शीर्षों के कोणीय उन्नयन को पूरक पाता है, तो छोटे पोल की ऊँचाई (मीटर में) है
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 14


दी गई जानकारी के अनुसार, BC = x मीटर,
ध्यान दें कि E BC का मध्य बिंदु है
∴ BE = EC = x/2 मीटर
मान लें कि खंभा AB की ऊँचाई = h मीटर
∴ खंभा CD की ऊँचाई = 2h मीटर
और, ∠AEB और ∠DEC समपूरक हैं।
∴ ∠AEB = (90° – Θ) और ∠DEC = Θ
त्रिकोण ΔABE में,


[∵ tan (90° – Θ) = cot Θ]
अब, त्रिकोण ΔCDE में,

दोनों समीकरण (i) और (ii) को गुणा करके,

इसलिए, विकल्प A सही है।

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 15
Save

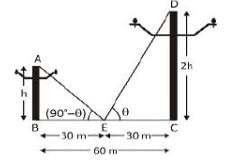
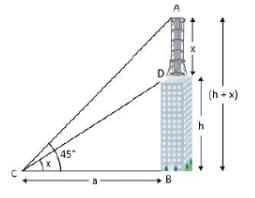
एक स्थान से एक भवन के शीर्ष और भवन की छत पर चिमनी के शीर्ष के लिए ऊँचाई का कोण क्रमशः x° और 45° है। भवन की ऊँचाई h मीटर है। तब चिमनी की ऊँचाई (मीटर में) है:
Detailed Solution for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 - Question 15

दिया गया है, भवन की ऊँचाई, BD = h मीटर
चिमनी की ऊँचाई, AD = x मीटर
और, BC = a मीटर
इसलिए, AB = BD + AD = (h + x) मीटर
ΔABC में,
चित्र
चित्र
a = h cot x ...(ii)
समीकरण (i) और (ii) से,
x + h = h cot x
x = h cot x – h
इसलिए, विकल्प B सही है।

142 videos|172 docs|185 tests
Join Course
Information about MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 Page
In this test you can find the Exam questions for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2, EduRev gives you an ample number of Online tests for practice
142 videos|172 docs|185 tests
Join Course
Download as PDF

Important Questions for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2

Find all the important questions for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 at EduRev.Get fully prepared for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 resources.

MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2

Prepare for the MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 within the RRB NTPC/ASM/CA/TA exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 Mathematics for RRB NTPC (Hindi)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ परीक्षण: ऊँचाइयाँ और दूरियाँ - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup