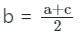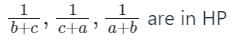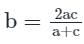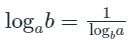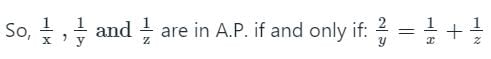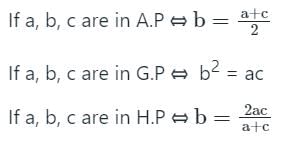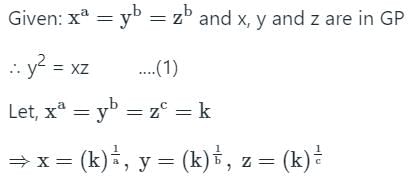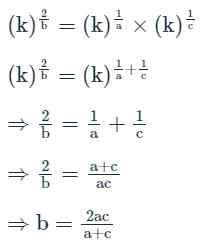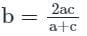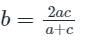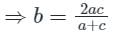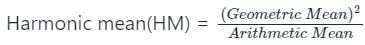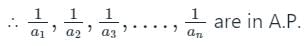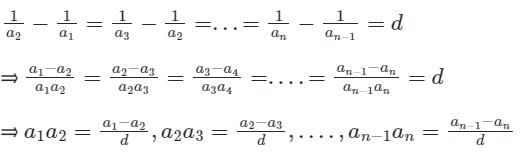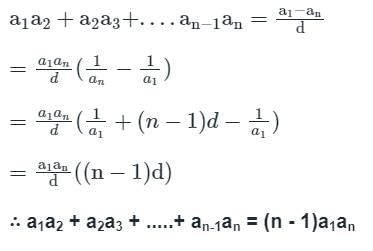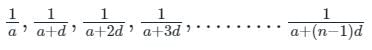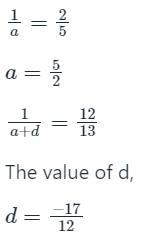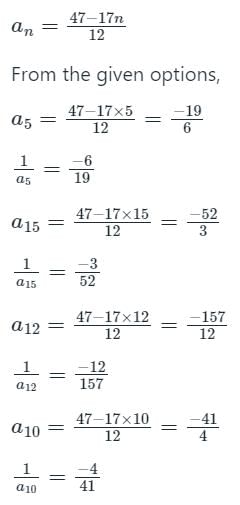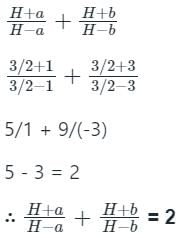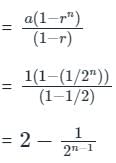MCQ: हार्मोनिक प्रगति - Bank Exams MCQ
15 Questions MCQ Test - MCQ: हार्मोनिक प्रगति
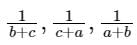 यदि a, b, c HP में हैं, तो निम्नलिखित में से कौन सा/से सही है?
यदि a, b, c HP में हैं, तो निम्नलिखित में से कौन सा/से सही है?
1. a, b, c AP में हैं
2. (b + c)2, (c + a)2, (a + b)2 GP में हैं। नीचे दिए गए कोड का उपयोग करके सही उत्तर का चयन करें।
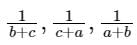 यदि a, b, c HP में हैं, तो निम्नलिखित में से कौन सा/से सही है?
यदि a, b, c HP में हैं, तो निम्नलिखित में से कौन सा/से सही है?यदि a, b, c एक ज्यामितीय प्रगति में हैं, तो logax x, logbx x और logcx x में हैं
तीन संख्याएँ 5, p और 10 हार्मोनिक प्रोग्रेशन में हैं यदि p = ?
यदि दो श्रृंखलाओं 3 + 10 + 17 + ... और 63 + 65 + 67 + ... के nth पद समान हैं, तो n का मान क्या होगा:
यदि xa = yb = zc हैं और x, y और z GP में हैं, तो a, b और c किसमें हैं?
यदि 1/2, 1/x, 1/8 हर्मोनिक प्रोग्रेशन में हैं, तो x का मान क्या है?
यदि समीकरण a (b - c) x2 + b (c - a) x + c (a - b) = 0 की जड़ें समान हैं, तो निम्नलिखित में से कौन सा सही है?
दो संख्याओं का गणितीय माध्य 14 और ज्यामितीय माध्य 12 है। संख्याओं का हार्मोनिक माध्य क्या है?
यदि a1, a2, a3, ........ एच.पी. में हैं, तो अभिव्यक्ति a1a2 + a2a3 +...... + an - 1an के बराबर है:
यदि एक हरित श्रेणी (H.P) के पहले दो पद 2/5 और 12/13 हैं, तो सबसे बड़ा पद है
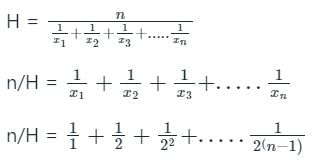
यदि H संख्याओं 1, 2, 22, 23, ......2n-1 का हार्मोनिक माध्य है, तो n/H का मान क्या होगा?


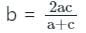 और इसके विपरीत
और इसके विपरीत